[통계학의 이해Ⅰ] 12주차 표집분포 -1. 표본평균의 표집분포

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 통계량의 확률분포인 표집분포에 대해 알아본다.
• 표본평균의 통계적 성질을 유도해본다.

---

표집분포(sampling distribution)

1. 통계량의 확률분포
   • 통계량: 측정 가능한 확률표본의 함수, 미지의 모수는 포함되지 않음
   • 관심 통계량

통계학의 이해Ⅰ 강의 자료 12-1 페이지1

• 순위의 경우 비모수통계량이다.

확률분포가 다음과 같을 때

통계학의 이해Ⅰ 강의 자료 12-1 페이지2

통계학의 이해Ⅰ 강의 자료 12-1 페이지2

• 위와 같은 확률분포를 갖는 경우 평균과 분산을 계산하면 저렇게 나온다.
• 두 개의 확률표본을 추출한 경우, 두 표본의 평균인 X bar의 분포는?

통계학의 이해Ⅰ 강의 자료 12-1 페이지3

• 2개의 확률표본을 추출한 경우 iid이다. 따라서 각각의 확률의 곱으로 표현 가능하다.
• 해당 상황에서 두 표본의 평균의 평균과 분산은 어떻게 구하나?

통계학의 이해Ⅰ 강의 자료 12-1 페이지3

• 채워지는 빈칸들은 독립이기 때문에 각각의 곱으로 구할 수 있따.

통계학의 이해Ⅰ 강의 자료 12-1 페이지3

• 해당 표본 평균은 각각 (x1 + x2) / 2가 나오는 값들을 구할 수 있고 해당되는 값들을 모두 합하여 분포를 구할 수 있다.
• 그렇게 구해진 표본평균의 분포의 기댓값과 분산을 구하면, 기댓값의 경우 동일한 형태이고, 분산의 경우 기존에 1/2를 곱한 형태이다.

통계학의 이해Ⅰ 강의 자료 12-1 페이지4

• 이를 일반화하여 n개를 추출했을 때도 구할 수 있다.
• 기댓값의 경우 아래 과정으로 구할 수 있다.

• 분산의 경우 아래 과정으로 구할 수 있다.

• 표준편차는 분산에 루트를 취한 형태로 구할 수 있다.
• 특별히 통계량의 표준편차를 표준오차 (standard error, SE)라고 한다.
  • 즉, 모집단의 표준편차를 표준오차라고 하는 것
• 분포의 형태는 기존의 것과 달라진다. 구조 및 형태가 달라지는 것이며 다양하게 바뀔 수 있다.

정규분포인 경우 (모집단의 분포가 정규분포인 경우)

통계학의 이해Ⅰ 강의 자료 12-1 페이지5

• X1과 X2가 정규분포를 따르면 그들의 선형결합도 정규분포를 따른다.

통계학의 이해Ⅰ 강의 자료 12-1 페이지5

• 정규분포인 경우 표본평균의 분포는 정규분포를 따른다.
• 표본평균의 평균은 본래 모집단의 평균이다.
• 표본평균의 분산은 본래 모집단의 분산에 n을 나눠준 형태이다.

통계학의 이해Ⅰ 강의 자료 12-1 페이지5

• 정규분포인 경우 표준화를 해서 문제를 해결하는 경우가 많은데, 표준화를 하면 표본평균의 분포는 결국 분산에 영향을 준다는 것을 알 수 있다.

지수족(exponential family): 정규분포포함

통계학의 이해Ⅰ 강의 자료 12-1 페이지6

• 지수족인 경우 합을 가지고 분포의 성질을 유도할 수 있다.
• 합은 표본평균으로도 표현이 되니 이를 이용하여 여러 성질을 유도할 수 있다.
• 감마분포는 모수가 알파와 베타인데, 알파는 모양을 나타내서 shape parameter, 베타는 척도를 나타내서 scale parameter 라고 한다.
• 다른분포를 유도할 때는, 직접 유도하거나 근사분포 유도를 하거나, 몬테카를로 모의실험을 통해 표집분포 추정하는 방법이 있다.
  • 요즘은 컴퓨터 계산이 많이 발달하여 몬테카를로 모의실험을 많이 사용

통계학의 이해Ⅰ 강의 자료 12-1 페이지7

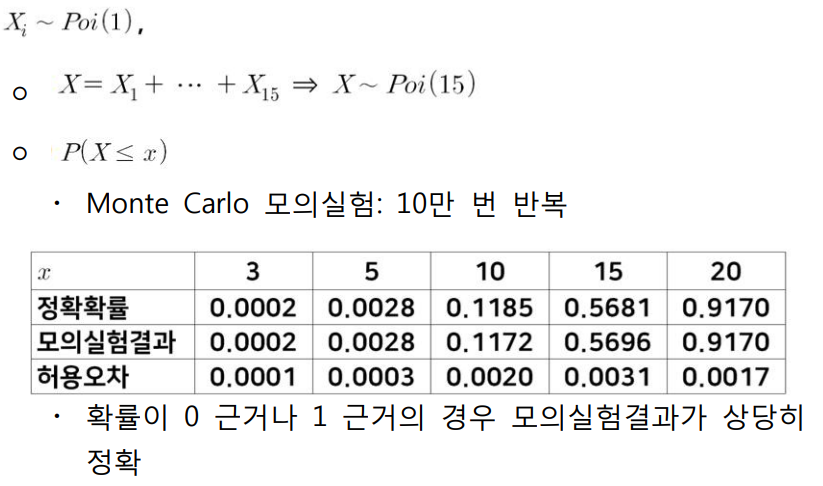
• 허용오차는 실제값과 벗어날 수 있는 영역에서 이정도 내에 오차가 있다는 것

---

요약

• 표집분포: 통계량의 (모집단) 분포
• 정규확률표본의 표본평균의 분포는 정규분포
• 독립인 지수족 표본들 합의 분포는 해당 지수족의 분포
• 기타 다른 분포는 직접 계산하거나 중심극한정리를 이용해서 근사정리를 할 수 있다.