[통계학의 이해Ⅰ] 11주차 정규분포 -1. 정규분포와 확률계산

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 통계학분야에서 가장 중요한 분포인 정규분포에 대해 알아본다.
• 정규분포의 확률과 분위수를 계산하는 과정을 설명한다.

---

정규분포(Normal Distribution)

• 이항분포가 대표적인 이산확률분포라고 하면 정규분포는 대표적인 연속확률분포이다.
• 정규분포는 De Moivre(1667 ~ 1754)가 이항분포에 대한 근사식을 유도하는 과정에서 발견
• 이후 Gauss(1777 ~ 1855)는 물리학 실험에서 발생하는 계측오차의 형태가 실험의 종류와 관계없이 비슷한 모양을 가지는 것 발견
• 이 계측오차의 분포로서 정규분포 제시 → 이때문에 정규분포를 가우시안분포 (Gaussian Distribution)라고도 함
• 정규분포라는 이름은 1893년 피어슨에 의해 붙여짐

통계학의 이해Ⅰ 강의 자료 11-1 페이지1

• 위 식이 정규분포의 확률밀도함수이다. 여기서 μ는 평균, σ^2은 분산, σ은 표준편차이다.
• C. F. Guass
  • 1809: 최소제곱법(method of least squares)의 개념 소개 → ∑(xi - a)^2이 최소가 되는 a가 xbar라는 것 산술평균
  • 위치모수의 추정값으로 산술평균이 적절함(오차의 정규법칙)을 보이는 과정에서 정규분포의 밀도함수 형태를 유도
• M. Laplace
  • 1774: 자료를 병합하는 문제 → Laplacian(이중지수) dist → ∑|xi - a|로 절댓값 형태로 측정
  • 1782: 아래 식 
  • 1810: 중심극한정리

통계학의 이해Ⅰ 강의 자료 11-1 페이지2

• K. Pearson: normal 본격적으로 사용 (표준편차 σ)

μ와 σ^2에 따른 정규분포의 확률밀도함수 → X ~ N( μ, σ^2 )

통계학의 이해Ⅰ 강의 자료 11-1 페이지3

• μ: 분포의 중심 ( -∞ < μ < ∞ ) → 평균 (= 중앙값 = 최빈값)
  • 위치를 결정, μ가 커질수록 분포의 중심위치는 오른쪽으로 이
• σ^2: 퍼져있는 정도 (σ^2 > 0) → 분산
  • σ가 커질수록 폭이 점점 넓어지는 형태
• 정규분포에서는 평균과 분산이 정규분포의 모양을 결정하는 모수이다.
• 정규분포의 확률밀도함수는 x = μ 일때 가장 큰 값
• x가 μ에서 멀어질수록 f(x)는 작아짐
• 평균 μ를 중심으로 대칭
• x축에서 특히 μ - σ와 μ + σ를 표기하는데, 이는 주요한 위치
  • 평균 μ에서 σ만큼 떨어진 지점은 f(x)가 오목인 상태에서 볼록인 상태로 변하는 변곡점

확률계산: P(a < X < b) = ?

통계학의 이해Ⅰ 강의 자료 11-1 페이지4

• 정규분포에서 칠해진 면적을 구하는 것이다.
• 하지만 식에 대입을 직접 계산할 수 없으며 수치해석학적으로 근사값을 구해야된다.
• 정규분포의 근사확률은 통계관련 프로그램이나 정규분포표를 이용하여 계산 가능
• 정규분포표를 이용할 때에는 다양한 평균과 분산에 대해 모든 표를 제공하기 어려움
  • 통계학에서는 특별한 정규분포에 대한 확률표 하나만 제공하고 다른 경우에 대해서는 표준화를 통해 확률 구함

표준정규분포(Standard Normal Distribution)

• 평균이 0이고 분산이 1인 정규분포

통계학의 이해Ⅰ 강의 자료 11-1 페이지5

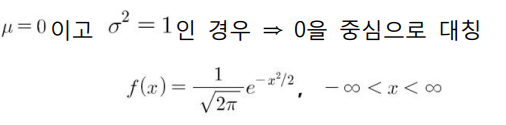
• 일반적으로 Z로 표시: Z ~ N(0, 1)
• 확률계산:

통계학의 이해Ⅰ 강의 자료 11-1 페이지5

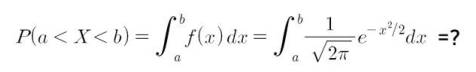
• 표준정규분포인 경우에도 쉽지 않으니, 통계프로그램이네 표로 계싼

통계학의 이해Ⅰ 강의 자료 11-1 페이지6

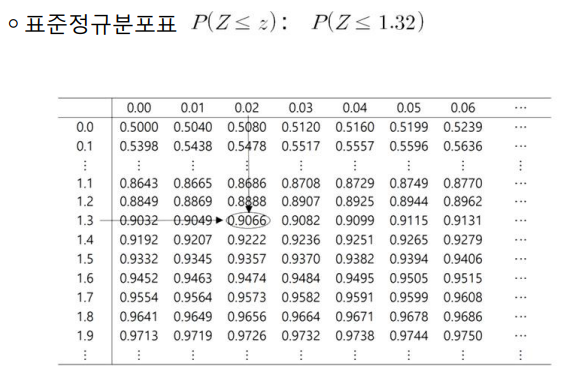
• 표준정규분포표는 소수점 둘째 자리 숫자 z에 대한확률 P(Z ≤ z)를 제공
• 표의 왼쪽 수직축에는 z의 소수점 첫째 자리까지의 숫자
• 표 위쪽 수평축에는 z.의 소수점 둘째 자리의 숫자 표시
• 표에서는 Z가 임의의 z보다 작거나 같을 확률만 제공하지만 이를 이용해 다양한 형태의 확률 계산 가능
• Z는 연속확률변수이므로 등호 포함 여부는 확률에 영향을 주지 않음

표준정규분포의 확률계산문제

• 0을 중심으로 대칭이라는 사실 이용
• 주요 형태

통계학 기본개념과 원리 제 2판 p201

통계학의 이해Ⅰ 강의 자료 11-1 페이지7

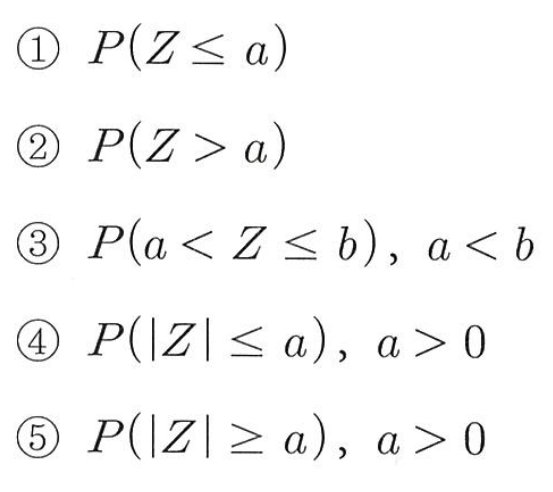
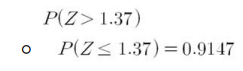
• 1.37보다 클 확률: Z가 1.37보다 작거나 같을 확률을 1에서 빼서 구할 수 있음

통계학의 이해Ⅰ 강의 자료 11-1 페이지7

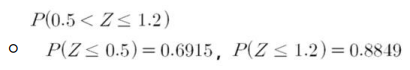
• 0.5와 1.2사이에 확률: Z가 1.2보다 작거나 같을 확률에서 0.5보다 작거나 같을 확률을 빼서 구할 수 있음

통계학의 이해Ⅰ 강의 자료 11-1 페이지7

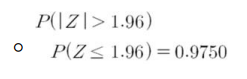
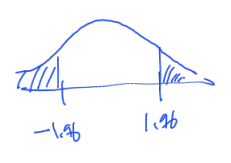
• 절댓값 Z가 1.96보다 클 확률: Z가 1.96보다 작거나 같을 확률을 1에서 뺀 뒤 2를 곱해 줌

α가 주어지고 P(Z > z) = α를 만족하는 z(분위수)를 계산

통계학의 이해Ⅰ 강의 자료 11-1 페이지9

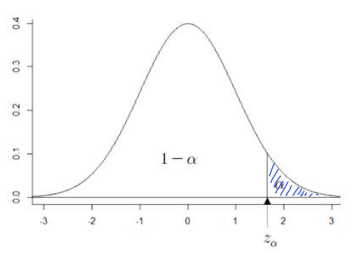
• P(Z < z) = 0.975를 만족시키는 z는?

• P(-z < Z < z) = 0.90를 만족시키는 z는?

 

---

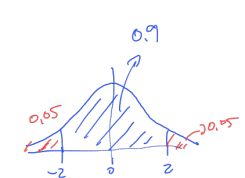
요약

• 정규분포의 모수는 평균과 분산이다.
• 정규분포는 평균 μ를 중심으로 대칭이며, σ이 퍼짐 정도를 나타낸다.
• 평균이 0, 분산이 1인 정규분포를 특별히 표준정규분포라고 한다.
• 표준정규분포의 확률을 구하기 어렵기 때문에 표준정규분포표를 제공한다.