[통계학의 이해Ⅰ] 10주차 주요 이산확률분포 Ⅱ-3. 다항분포

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 이항분포의 확장된 형태인 다항분포의 성질에 대해 알아본다.

---

도수분포표(Frequency table)

• 범주형 자료 또는 범주화된 자료를 정리
• 각 범주에 몇 개의 관측개체가 있는지를 정리한 표
  • 도수
  • 상대도수
    • 표본을 계속 뽑으면
    • 해당범주가 모집단에서 차지하는 비율(확률)로 수렴 → 해당 부분이 통계학에서의 관심사이다.

다항분포(Multinomial Distribution)

• 각 시행에서 발생 가능한 결과는 k가지
  • 이항분포는 결과가 성공 또는 실패의 2가지 경우
  • 다항시행(multinomial trial)에서 결과는 k개의 서로 배반인 범주 중의 하나에 속함
• 각 시행에서 i번째 결과의 확률은 Pi로 고정
  • 따라서 i는 1부터 k까지 모든 pi의 합은 1이다.
• 각 시행은 독립적으로 수행
• (X1, X2, ..., Xk): n번 시행했을 때, 각 결과의 횟수

통계학의 이해Ⅰ 강의 자료 10-3 페이지3

• Xij: i번째 시행에서 결과 j가 나오면 1 아니면 0
  • Xij = 1이면, Xil = 0, l ≠ j
  • 가로를 보았을 때 각각의 X1j, X2j, ..., Xnj는 1은 1개씩 있으며 나머지는 0이기 때문에 합은 1이다.
• i1 ≠ i2인 경우 Xi1j1과 Xi2j2는 서로 독립
  • 따라서 공분산은 0이다.
  • 앞에 첨자 (i)가 다르면 그 외 첨자들은 모두 독립이다.

다항분포의  확률질량함수는 이항분포에서 유도할 수 있다.

이항분포

통계학의 이해Ⅰ 강의 자료 10-3 페이지4

• X1의 관점에서 본다면, x1과 나머지로 분류하여 이항분포로 생각할 수 있다.
• 확률이 p1이고 시행횟수가 n인 이항분포이다.

통계학의 이해Ⅰ 강의 자료 10-3 페이지4

• 따라서 X2는 X1을 제외한 나머지 범주로 표현할 수 있다. X2 = n-X1, p2 = 1-p1으로 표현
• 이를 기반으로 다항분포의 확률질량함수는 확장시켜서 유도할 수 있다.

다항분포

통계학의 이해Ⅰ 강의 자료 10-3 페이지4

예제

멘델의 유전법칙

• 독립의 법칙: 완두의 껍질 모양(R, r), 색깔(Y, y)
  • RRYY, rryy인 완두 교배 1대를 자기수분시킨 2대의 발현 비율
    • RY:Ry:rY:ry = 9"3"3"1
• 독립적으로 n개의 2대를 얻었을 때, (RY, Ry, rY, ry)에 속한 완두의 수를 (X1, X2, X3, X4)라고 하면

통계학의 이해Ⅰ 강의 자료 10-3 페이지5

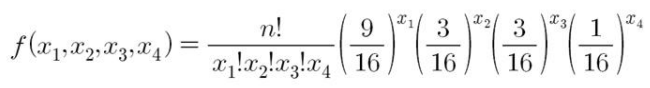
• 특정 결과에만 관심이 있는 경우,
  • 예) i-번째 결과 (Ri)에만 관심 → 나머지 결과를 묶음 (Ri^c)
    • Xi ~ N(n, pi)
    • E(Xi) = npi
    • Var(Xi) = npi(1-pi)
  • 예) i-번째 또는 j-번째 결과 (Ri ∪ Rj)에만 관심 있는 경우,
    • Y = Xi + Xj ~ B(n, pi + pj)
    • E(Y) = E(Xi + Xj) = n( pi + pj)
    • Var(Y) = Var(X1 + X2) = n(pi + pj)(1 - (pi + pj))

공분산 

• 만약 X1과 X2의 공분산을 알고싶다면, 모든 공분산을 다 구해준 뒤 더한다.
• Cov(X11 + X21, X12 + X22)
  = Cov(X11, X12) + Cov(X11, X22) + Cov(X21, X12) + Cov(X21, X22)
  → 여기서 앞에 첨자가 다르면 독립이기 때문에 해당 공분산은 0이된다.

통계학의 이해Ⅰ 강의 자료 10-3 페이지7

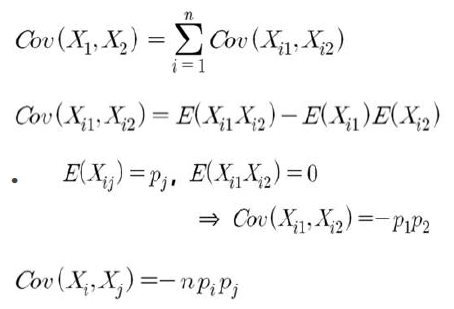
상관관계

통계학의 이해Ⅰ 강의 자료 10-3 페이지8

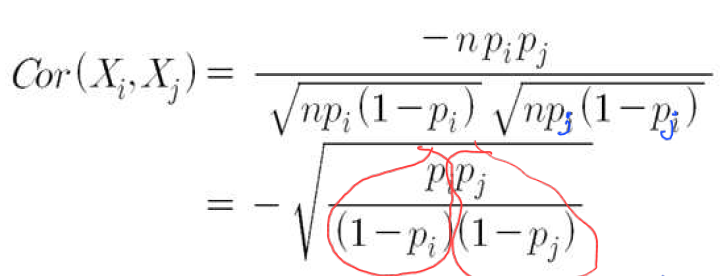
• 각 범주 빈도에 해당되는 상관계수는 이처럼 표시된다.
• 성공확률 / 실패확률 형태
  • 이러한 형태를 오즈(odd)라고 따로 명칭한다 

분산

통계학의 이해Ⅰ 강의 자료 10-3 페이지8

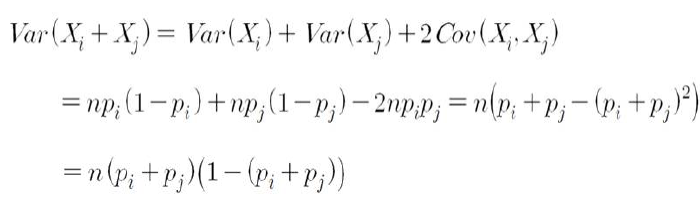
예제

멘델의 유전법칙

• 모양 (R, r)에만 관심이 있는 경우, R:r = 12:4 = 3:1
  • R의 개수: Y = X1 + X2 ~ B(n, 0.75)
• 100개의 완두에 대해 우성인자만 있는 경우와 열성인자만 있는 완두 수의 상관계수는?

통계학의 이해Ⅰ 강의 자료 10-3 페이지9

통계학의 이해Ⅰ 강의 자료 10-3 페이지10

---

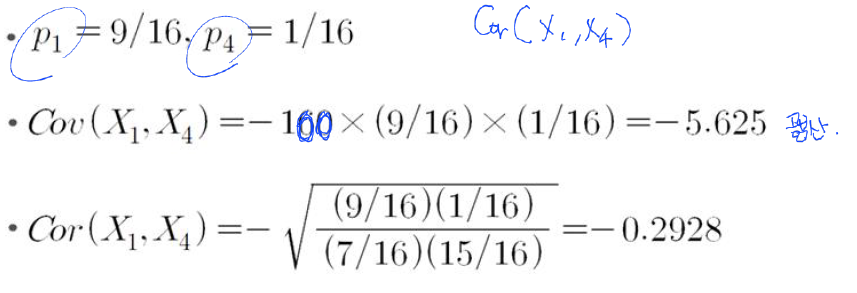
요약

• 다항분포
  1. 각 시행에서 발생 가능한 결과는 k가지
  2. 각 시행에서 i번째 결과의 확률은 pi로 고정
  3. 각 시행은 독립적으로 수행
  4. n번 시행했을 때 각 결과의 횟수 분포
  5. 특정 결과의 횟수 분포 → 이항분포

통계학의 이해Ⅰ 강의 자료 10-3 페이지11

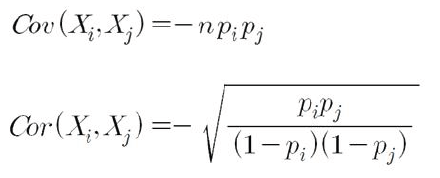
• 이항분포인 경우 p와 (1-p) 두가지 이기 때문에 대입하면 상관계수가 -1이 나온다.
  • 하나가 발생하면 반대는 발생하지 않는 직선관계를 갖는 것