[통계학의 이해Ⅰ] 9주차 주요 이산확률분포 Ⅰ-3. 초기하분포

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 유한모집단이 두 그룹으로 나누어져 있고 표본을 비복원으로 추출할 때, 특정 그룹에서 뽑힌 표본의 수에 대한 확률분포를 알아본다.
• 초기하분포의 성질과 관련 문제에 대해 알아본다.

---

초기하분포 (Hypergeometric Distribution)

• 크기가 N인 모집단이 크기가 M과 N-M인 두 개의 부모집단 (A, B)로 나누어진 경우 → 유한모집단
• n개의 표본을 비복원으로 추출할 때, 부모집단(A)에서 추출될 표본 수의 분포
  • 각 표본의 추출과정은 독립적이지 않음
• 따라서 유한한 모집단에서 두 그룹으로 나누어져 있을 때 표본을 비복원추출하는 경우 나오는 분포

예제

• 6개의 정상품과 4개의 불량품이 있는 상자에서 임의로 3개의 제품을 비복원 추출한 경우에 3개 중 1개가 불량품일 확률?
  • 3개 중 1개가 불량품일 사건:
    • {(불, 정, 정), (정, 불, 정), (정, 정, 불)}
    • P(불, 정, 정) + P(정, 불, 정) + P(정, 정, 불)

통계학의 이해Ⅰ 강의 자료 9-3 페이지1

• 모든 확률을 곱하고 더하는 과정에서 결국 분모는 10 * 9 * 8, 분자는 6 * 5 * 4를 따르며, 총 3개가 존재하는 형태이다.
• 따라서 3개의 위치 중 하나를 선택해 "불"을 대입하는 방법의 수에서 유도된 것
• 분자에서 4는 4개에서 1개를, 6 * 5는 6개에서 2개를 비복원 추출 나열하는 방법
• 분모는 10개에서 3개를 비복원추출 나열하는 방법

통계학의 이해Ⅰ 강의 자료 9-3 페이지3

 

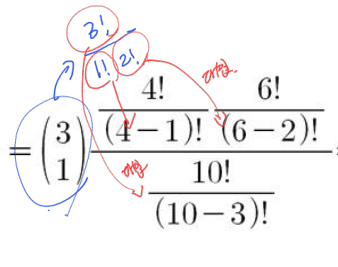
• 중간 과정에서는 해당 것들을 대입하여 최종 형태로 표현 가능
• 따라서 해당 경우 x에 따른 확률질량함수는 아래와 같다

통계학의 이해Ⅰ 강의 자료 9-3 페이지4

• 이러한 형태를 초기하분포의 확률질량함수라고 한다.

초기하분포 확률질량함수 일반식

통계학의 이해Ⅰ 강의 자료 9-3 페이지5

• M: 관심이 있는 모집단의 수
• N: 전체 모집단의 수
• n: 표본의 수
• x: 관심있는 표본의 수
  • 해당 식에서 분모의 값은 전체 N개 중 n개의 표본을 선택하는 조합의 수
  • 분자의 값은 불량품 M개에서 x개를 선택하고 정상품 N-M개에서 n-x를 선택하는 조합의 수
  • 위와 같은 확률질량함수를 가지는 분포를 초기하분포라고 함
• 보통의 경우 X가 가질 수 있는 값은 0~n으로 표시할 수 있으나, n이 불량품의 수 M보다 클 수 없기 때문에 X의 최댓값은 n과 M 중 작은 값인 min(n, M)이 된다.
• n이 정삼품의 수 N-M보다 크면 최소한 n-N+M개의 불량품이 반드시 선택되기 때문에 X의 최솟값은 max(0, n-N+M)이 된다.
• X는 모수가 (N, M, n)인 초기하분포를 따른다고 하며 X ~ H(N, M, n)으로 표기
• N이 크고 N에 비해 n이 상대적으로 작은 경우
  • 비복원의 효과가 적기 때문에 베르누이 실험으로 근사모형 가능
  • 초기하분포는 p=M/N인 이항분포로 근사 (비복원 효과가 미미하기 때문에 복원에 근사)

예제

• 10000개의 제품 중 7000개가 정상, 3000개가 불량일 때, 3개를 비복원 추출해서 불량품이 한 개일 확률

통계학의 이해Ⅰ 강의 자료 9-3 페이지6

• N이 크고 .n이 작을 경우 비복원 추출하여 두 번째 추출한 7000/9999는 복원추출인 7000/10000와 크게 차이가 없다.
• 정확하게 보자면 왼쪽은 초기하분포, 오른쪽은 이항분포이지만, 해당 경우처럼 N이 매우크고 상대적으로 n이 작은 경우 이항분포로 보고 풀어도 큰 문제가 없다.

초기하분포의 기댓값과 분산

• 초기하분포의 평균과 분산도 이항분포의 평균과 분산을 계산할 때처럼 각 실험의 결과의 합으로 생각하면 쉽게 유도 가능
• 초기하분포도 각 시행에서 A집단에서 추출되면 1, 다른 집단에서 추출되면 0으로 표시한 확률변수의 합

통계학의 이해Ⅰ 강의 자료 9-3 페이지7

• 이항분포와 다른 점은 서로 독립이 아니라는 것이다.
•  하지만 i = 1, ..., n에 대해 Xi의 확률은 동일하다.

통계학의 이해Ⅰ 강의 자료 9-3 페이지7

• 따라서 초기하분포의 기댓값은 아래와 같다.

통계학의 이해Ⅰ 강의 자료 9-3 페이지8

• Var(Xi)는 위와 같게 나오지만 추출이 비복원으로 각각의 시행이 독립이 아니다.
• 따라서 모든 Var(Xi)의 합으로 Var(X)를 표현할 때에는 공분산을 고려해줘야 된다.

통계학의 이해Ⅰ 강의 자료 9-3 페이지8

• 공분산에 대한 수식은 아래처럼 풀 수 있다.

통계학의 이해Ⅰ 강의 자료 9-3 페이지9

• 해당 식으로 정리한 공분산을 다시 X의 분산을 구하는 식에 대입하면 아래와 같다.

통계학의 이해Ⅰ 강의 자료 9-3 페이지10

• 초기하분포에서는 최소 하나 이상을 뽑는 것이기 때문에 이항분포에서 나온 분산보다 초기하분포의 분산이 작거나 같다.
• 초기하분포의 분산은 이항분포의 분산에 N-n/N-1을 곱한 형태이다.
• 해당 분산 식에서 N이 엄청 커지고 n이 작아지게 되면 N-n/N-1이 1에 가까워지면서 초기하분포의 분산이 이항분포 분산에 근접해진다.
• 따라서, N-n/N-1을 유한모집단 수정계수 라고 하며, 1보다 작거나 같다.
• 초기하분포의 분산은 이항분포의 분산보다 작아 통계적으로 더 안정적인 결과를 얻을 수 있기 때문에 표집검사에서는 복원추출보다는 비복원추출에 의한 검사를 많이한다.
• 이항분포와 초기하분포의 차이는 모집단이 무한이냐 유한이냐 하는 것
• 유한개의 개체로 이루어진 모집단이더라도 복원추출한다면 무한개의 표본을 뽑을 수 있기 때문에 모집단은 무한하다고 볼 수 있음

예제

품질관리 - Operating Characteristic(OC) curve

• 50개의 전구들이 들어있는 상자에서 10개의 전구를 무작위로 선택하여 검사
• 불량전구의 개수가 1개 이하이면 이 회사의 전구를 구매
• 만약 이 상자에 5개의 불량품이 있을 때, 구매할 확률은?
  • X = 10개 중 불량품의 수

통계학의 이해Ⅰ 강의 자료 9-3 페이지11

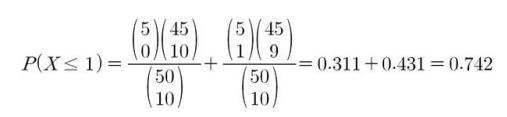
• 만약 k개 불량품이 있을 때 구매할 확률은?
  • 해당 경우에는 k에 따라서 확률을 표시할 수 있음
  • 이처럼 k와 확률의 함수로 곡선으로 연결하면 그래프를 얻을 수 있으며, 이를 검사특성곡선(operating characteristic curves, OC 곡선)이라 함

통계학의 이해Ⅰ 강의 자료 9-3 페이지12

• OC curve 계산
  • OC curve를 기준으로 몇 개의 표본을 추출할 것인지
  • 불량품이 몇 개일때까지 구매할 것인지 등 확인 가능

연못에 사는 물고기는 몇 마리?

• 꼬리표를 붙인 20마리의 물고기를 연못에 넣고 어느 정도 지난 후 물고기 15마리를 잡았을 때 꼬리표가 있는 물고기의 분포는?
  • N-20: 꼬리표가 없는 물고기
  • 해당 경우는 물고기가 무한정 많을 수 없으며, 뽑을때마다 줄어들기 때문에 비복원이다.
  • 따라서 초기하분포로 설명할 수 있으며, 전체 마리수가 N이면, N-20이 꼬리표가 없는 물고기의 수이다.

• 만약 15마리 중 4마리가 꼬리표가 있는 물고기라면?

• 따라서 N = 75이다.
  • 해당 경우 비례식으로 계산할 수 있지만, 확률적 모형인 초기하분포를 통해 설명할 수 있다.

---

요약

• 크기가 N인 모집단이 두 그룹 (크기가 M과 N-M)으로 나뉘고 n개의 표본을 비복원으로 추출할 때, 특정 그룹에서 추출될 표본 수의 분포

통계학의 이해Ⅰ 강의 자료 9-3 페이지16

• n << N인 경우 p=M/N인 이항분포로 근사할 수 있음
• 초기하분포의 기댓값과 분산

통계학의 이해Ⅰ 강의 자료 9-3 페이지16