공부하는 블로그
[통계학의 이해Ⅰ] 9주차 주요 이산확률분포 Ⅰ-2. 이항분포 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.
학습목표
- 대표적인 이산분포인 이항분포의 성질에 대해 알아본다.
이항분포 (Binomial distribution)
- 성공할 확률이 p인 베르누이 실험을 n번 반복했을 때, 성공 횟수(X)의 분포
- Xi ~ B(p)라고 할 때, 성공 횟수 X는 n개의 베르누이 확률변수를 합으로 표시
- Xi는 i번째 베르누이 시행 결과
- 확률변수 Xi는 각각의 베르누이 시행 결과이며 X는 확률변수의 합으로 표현 가능

이항분포의 기댓값과 분산

- 베르누이 확률변수의 기댓값으로 이항분포의 기댓값을 유도할 수 있음
- i번째 베르누이 확률변수의 기댓값은 성공할 확률인 p이다.
- 이항확률변수의 기댓값은 모두 합친 것의 기댓값인데, 이는 각각의 기댓값의 합으로 표현 가능
- 따라서 이항확률변수의 기댓값은 np가 된다.
- 분산또한 베르누이 확률변수의 분산으로 유도 가능
- 베르누이 시행은 독립이고, 독립일 때에는 공분산이 0이다.
- 두 확률변수의 합의 분산은 각각의 분산을 더하고 2배한 공분산을 빼는 것임
- 공분산이 0이기 때문에 각각의 분산의 합으로 표현 가능
- 따라서 이항확률변수의 분산은 np(1-p)이다.
예제
주사위 세 번 던지기: X = 1이 나온 횟수

- 해당되는 확률을 계산할 때, 1과 2의 경우 각 원소의 확률이 동일하기 때문에 해당되는 원소의 개수를 계산하여 곱해주면 된다.
- 이를 일반화하여 확률질량함수를 구할 수 있음
시행횟수 n, 성공확률 p인 이항분포의 확률질량함수

- n과 p에 따라 확률이 달라짐
- 이항분포의 모양을 결정
- 분포의 특성을 완전히 결정하는 모수임
- X ~ B(n, p)로 표현
- 베르누이 확률변수의 경우 n=1이므로 X ~ B(1,p)로도 표기 가능
예) n = 8일 때,
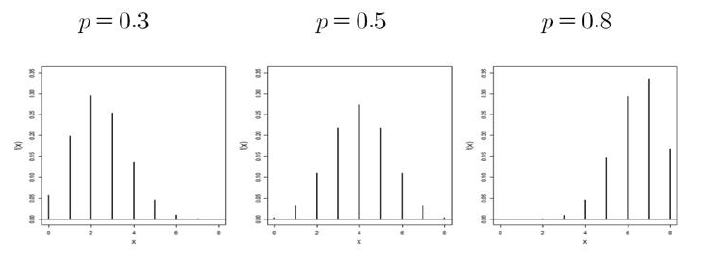
- n이 8로 고정되어 있을 때, 확률 p에 의해 모형이 다 달라짐
- 0.5일 경우 가운데를 중심으로 대칭 형태이다 (n = 1일때와 7일때 동일값 확인 가능)
- p = 0.3일 경우 왼쪽으로 모여있으며, 0.8인 경우는 오른쪽에 모여있음
- n이 변경되도 모형이 달라진다.
- 통계학 문제: 모수(주로 p)는 얼마인가?
- 주로 통계학에서는 p가 무엇인지에 관심을 갖는다.
- 이러한 것들을 데이터를 통해서 추론할 수 있음
- 누적으로 X가 x보다 작거나 같은 확률의 경우 x이하의 값들을 모두 합하여 구할 수 있음
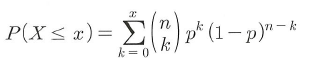
예제
항암제 완치율
- 어떤 암에 대한 기존 항암제의 완치율은 50%
- 어느 제약회사에서 새로운 항암제를 개발하여 항암제의 효과를 확인하기 위해 15명의 환자를 대상으로 임상시험
- 만약 새로운 항암제의 완치율이 기존과 같다면?
- 8명이 완치될 확률은?
- 15명의 환자는 서로 상관관계가 없으므로 베르누이 시행
- p=0.5일 때 X = 8일 확률을 구하는 것.
- 따라서 0.196
- 8명이 완치될 확률은?
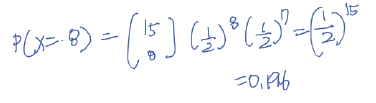
- 적어도 10명 이상 치유될 확률은?
- P가 10이하일 경우를 모두 구해서 더하는 것
- 따라서 0.151
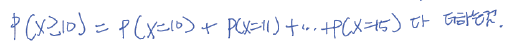
- 통계학 문제: 환자 중 12명의 환자가 치유되었다면, 새로운 항암제의 효과가 기존의 것보다 P(X ≥ 12)일 확률을 계산하면 0.018이 나온다.
- 유의수준은 나중에 통계학의 이해2에서 배움,,,
- 이 값이 작으면 작을수록 해당 case가 잘 나오지 않는 다는 것으로 가정한 것이 맞지 않다는 것...
윷의 젖혀질 확률
- A가 젖혀질 확률이 0.4인 윷을 4번 던지고 B도 같은 확률을 가지는 윷을 6번 던질 때 두 사람이 던진 윷 중 젖혀진 윷이 2개 이하일 확률은?
- X: A가 던진 윷 중 젖혀진 윷의 수, X ~ B(4, 0.4)
- Y: B가 던진 윷 중 젖혀진 윷의 수, Y ~ B(6, 0.4)
- X + Y ≤ 2 일 확률은?
- 이항분포의 중요한 성질 중 하나는 성공할 확률이 동일하고 서로 독립인 이항확률변수의 합도 이항분포를 따른다는 것
- 두 확률변수 X와 Y가 각각 X ~ B(m,p)와 Y ~ B(n,p)이고 서로 독립이라면 X+Y는 성공확률이 p인 베르누이 시행을 각각 m번과 n번 반복하여 더한 것이다. 따라서 X+Y ~ B(m+n, p)가 된다.
- 따라서 해당 문제에서 W = X+Y ~ B(10, 0.4)이다.
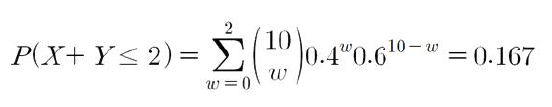
요약
- 이항분포: 성공확률이 p인 베르누이 시행을 n번 시행했을 때 성공 횟수의 분포
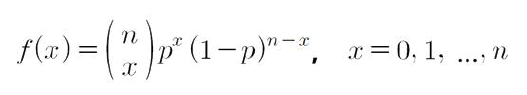
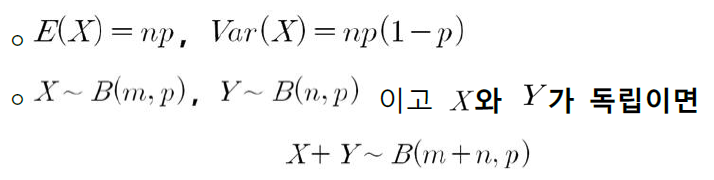
- 기댓값과 분산은 베르누이 시행을 통해 유추할 수 있음
- X와 Y가 이항분포이고 성공확률이 같으며 서로 독립일 때, 두 개의 합에 해당되는 것 또한 이항분포이며, 실행횟수를 합해주는 것
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 9주차 주요 이산확률분포 Ⅰ-4. 확률분포 실습 (2) | 2024.02.13 |
|---|---|
| [통계학의 이해Ⅰ] 9주차 주요 이산확률분포 Ⅰ-3. 초기하분포 (2) | 2024.02.13 |
| [통계학의 이해Ⅰ] 9주차 주요 이산확률분포 Ⅰ-1. 베르누이 시행과 확률변수 (2) | 2024.02.12 |
| [통계학의 이해Ⅰ] 8주차 확률벡터 -4. 결합분포 퀴즈 (0) | 2024.02.11 |
| [통계학의 이해Ⅰ] 8주차 확률벡터 -3. 공분산과 상관계수 (0) | 2024.02.11 |




