공부하는 블로그
[통계학의 이해Ⅰ] 6주차 조건부 확률 -3. 독립사건 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.
학습목표
- 독립사건의 정의와 관련 문제에 대해 알아본다.
독립사건(independent events)
- P(A ∩ B) = P(A)P(B|A) = P(B)P(A|B)
- A가 B에 영향을 안주고 B가 A에 영향을 주지 않는다면, P(B|A) = P(B), P(A|B) = P(A)
- 사건 A와 B가 서로 영향을 주고 받지 않는 경우, "사건 A와 B는 독립사건(independent events)이다."
- P(A ∩ B) = P(A)P(B)
- 두 사건이 독립인지 아닌지를 얘기할 때 P(A ∩ B)의 확률이 각각 A와 B 확률의 곱으로 표시될 수 있으면 독립사건이라고 하며, 성립되지 앟는 경와 A와 B는 서로 종사건이다 혹은 독립사건이 아니라고 한다.
- 또한 표본공간과 공집합은 임의의 사건 A와 독립이다.
- 표본공간의 확률은 1이고, 공집합의 확률은 0이기 때문에 곱하면 아래와 같이 나오는 것이다.
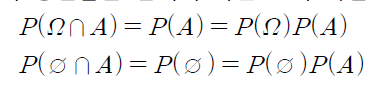
- 사건 A, B, C에 대하여 모든 곱사건의 확률이 해당 개별 사건 확률의 곱으로 표시되면 독립이다.
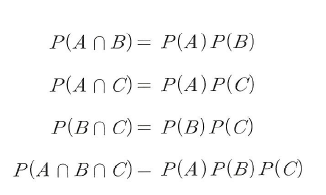
- 해당 식을 일반화하면, 일반적인 n개의 사건 A1, A2, ... , An이 서로 독립적이면 해당 사건들의 확률의 곱으로 표시된다.
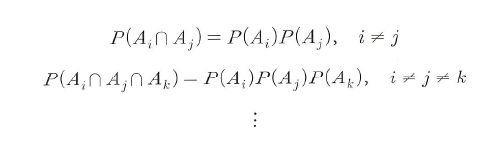
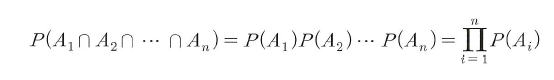
- 따라서 위의 식들이 모두 성립하면 A1, A2, ..., An이 서로 모두 독립적이다.
예제
- 동전 또는 주사위 2개 던지기
- 첫 번째 결과와 두 번째 결과는 서로 영향을 주지 않기 때문에 독립이다.
두 개의 정육면체 주사위
- A: 두 주사위의 합이 6인 사건
- B: 두 주사위의 합이 7인 사건
- C: 첫 번째 주사위가 3인 사건
- A = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
- B = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
- C = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)}
- Q. A와 C는 독립인가?
- P(A ∩ C) = P(A)P(C) 를 이용해서 풀이를 해보았을 때, 같지 않게 나오기 때문에 독립이 아니다.
- Q. B와 C는 독립인가?
- P(B ∩ C) = P(B)P(C) 를 했을 때 같게 나오기 때문에 B와 C는 독립이다.
- 위 예시에서는 A는 두 주사위의 합이6이기 때문에 첫 번째 주사위의 값에 6이 나오지 못하도록 영향을 미친다. 하지만 B는 합이 7인경우라서 첫 번째 주사위 값에 영향을 미치지 않는다. 따라서 A와 C는 독립이 아니고, B와 C는 독립이다.
- Q. A와 B가 득립이면?
- A와 B가 독립이면 A와 B의 여집합, A의 여집합과 B, A의 여집합과 B의 여집합 모두 독립이다.

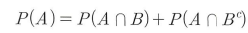
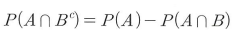

- Q. A와 B가 배반사건이면?
- 배반사건과 독립사건을 연결지어서 생각하려는 경향이 있는데, A와 B의 교사건이 공집합일 때 배반사건이다. 따라서 배반사건과 독립은 전혀 연결이 되지 않는다.
주사위 3개를 던지기
- 6이 최소한 한번 이상 나올 확률은?
- A: 주사위 눈이 6인 경우가 최소한 한번 이상 나올 사건
- Ai: i번째 주사위 눈이 6인 사건
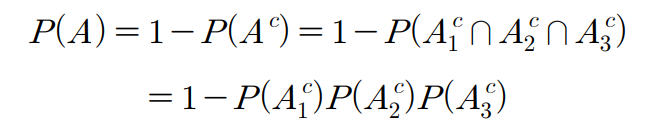
- 최소한 한번 이상 나올 사건의 경우 여사건으로 푸는 것이 훨씬 쉽게 풀 수 있다.
- 각각의 주사위를 던지는 사건은 독립사건이기 때문에 곱으로 풀어서 구하는 것이고, 따라서 값은 1-5/6 * 5/6 * 5/6이다.
전기전달시스템
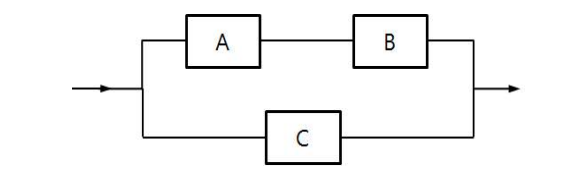
- 가정: 세 개의 ON/OFF 스위치로 구성 & 각각의 스위치는 독립적으로 세팅
- 스위치 A, B, C가 ON일 확률은 각각 0.7, 0.8, 0.6
- A와 B는 직렬, C와 A는 병렬로 구성
- 문제를 수식으로 표현하여 풀이를 하는 과정이 중요
- 직렬은 교집합으로 병렬은 합집합으로 표현
- 전기가 전달될 사건: C∪(A∩B)
- 가정: 각각의 스위치가 독립적으로 세팅
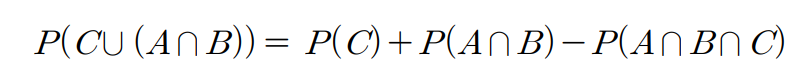
- 독립사건임을 이용하기 위해 "P(A∪B) = P(A) + P(B) - (A∩B)"를 활용하여 교집합으로 표기한 것
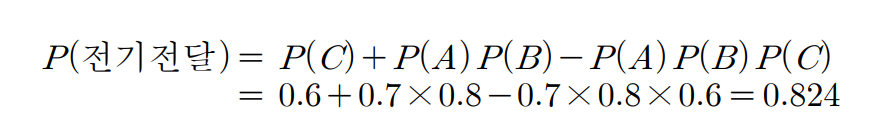
요약
- 사건 A와 B가 독립사건 (independent events)일 경우
- P(A∩B) = P(A)P(B)
- A와 B가 독립이면, A와 B의 여집합, A의 여집합과 B, A의 여집합과 B의 여집합 모두 독립이다.
- 직렬은 교집합으로 병렬은 합집합으로 표현한다. (수명은 직렬은 min으로, 병렬은 max로 표기)
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -5. 확률 퀴즈 설명 (0) | 2024.01.29 |
|---|---|
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -4. 베이즈 정리 (2) | 2024.01.29 |
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -2. 조건부 확률 (2) | 2024.01.22 |
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -1. 확률의 정리 (2) | 2024.01.22 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -4. 확률계산 실습(R) 및 퀴즈 (0) | 2024.01.21 |



