공부하는 블로그
[통계학의 이해Ⅰ] 6주차 조건부 확률 -1. 확률의 정리 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.
학습목표
- 확률의 공리를 기반으로 확률에 대한 기본정리(theorem)을 유도하고 예제를 통해 어떻게 응용될 수 있는지 알아본다.
공리적 확률 (Probability Axioms)
- 확률이론이나 통계이론을 유도하는데 있어 고전적 정의나 빈도학파적 정의로는 일반적인 확률의 이론을 도출하는 데 한계가 있다.
- 1993년 콜모고로프 (A. N. Kolmogorov, 1903-1987)가 확률의 공리를 발표하면서 확률이론이 체계를 이루게 된다.
- 표본공간상에서 아래의 공리를 만족하는 P()를 확률측도(probability measure)라고 하고 P(A)르 사건 A의 확률이라고 한다.

공리(axiom)란 증명할 수 없으나 옳다고 판단되는 명제
- 공리1은 어떤 실험의 결과는 표본공간 Ω에서 항상 일어남을 뜻한다.
- 공리2는 어느 사건도 확률이 음수가 될 수 없으며 1보다 클 수도 없음을 뜻한다.
- 공리3은 서로 배반사건인 두 서건 A와 B에 대해 합사건의 확률은 각각의 확률의 합과 같음을 의미한다.
확률의 기본정리
위 공리로부터 확률의 기본적인 성질을 설명할 수 있다.


- 첫 번째 성질은 A여집합의 확률은 1-A의 확률이라는 것이다. (반대도 적용)
- 해당 성질은 Ω = A ∪ A^c이며 A와 A여집합은 상호 배반이므로 공리1과 공리 3에 의해 증명 과정이 유도된다.
- 해당 성질을 이용하면 P(공집합) = 0 인 것을 쉽게 알 수 있다. (표본공간의 여집합은 공집합인 것)
예제
- 생일문제
- k명 중 적어도 두 사람 이상이 생일이 같을 확률
- A = k명의 사람이 모두 다른 생일을 가지는 사건
- 해당 A사건의 여사건이 적어도 두 사람 이상이 생일이 같을 확률인 것이다.
- 두 사람 이상 생일이 같을 확률은 두 사람, 세 사람... 이렇게 구해서 계산이 복잡해 지는데, 여사건을 이용하면 쉽게 풀 수 있다.
- 100장 중 4장이 당첨 복권
- 4장의 복권을 구입했을 때, 적어도 한 장 이상의 당첨복권을 구입하게 될 확률?
- A: 한 장 이상의 당첨복권을 구입할 사건
- 당첨복권이 한 장, 두 장, 세 장, 네 장인 경우
- A^c: 구입한 4장 모두 당첨되지 않을 사건


- 두 번째 성질은 사건 A가 사건 B의 부분사건이면 P(A) ≤ P(B) 이다.
- 벤다이어그램에 의해 B = A ∪ (B ∩ A^c) 로 표현할 수 있고, A와 (B ∩ A^c) 는 서로 배반사건이기 때문에 공리 3에 의하여 더하기로 표시할 수 있다.
- 공리2에 의해 (B ∩ A^c) ≥ 0 이므로 P(A) ≤ P(B)가 성립된다.
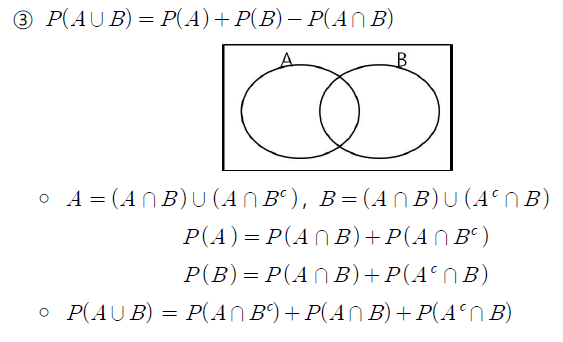
- 세 번째 성질은 P(A ∪ B) = P(A) + P(B) - P(A ∩ B) 이다.
- 공리 3은 A와 B가 서로 배반사건인 경우에 적용되는 것이고, 일반적인 경우에는 위 처럼 A와 B의 교집합이 공집합이 아닌 경우가 있다.
- 위 상황에서 A와 B에 대하여 각각 아래처럼 변형시킬 수 있다. (아래는 A만)
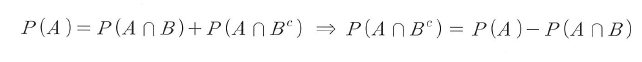
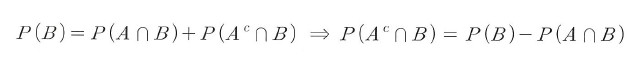
- 벤다이어그램 상에서 A와 B의 합사건은 아래처럼 표시할 수 있다.
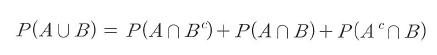
- 합사건으로 표현된 식에 각각 P(A ∩ B^c)와 P(A^c ∩ B)에 A와 B에 대해 유도한 식을 대입하면 세 번째 성질이 성립된다.
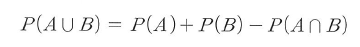
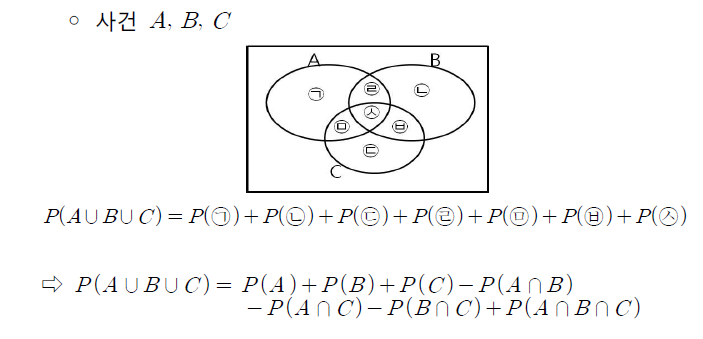
- 또한 사건이 3개, A, B, C라면 아래처럼 식이 성립된다.
- 즉 n개의 사건에 대해서는 일반화식을 유도할 수 있다.
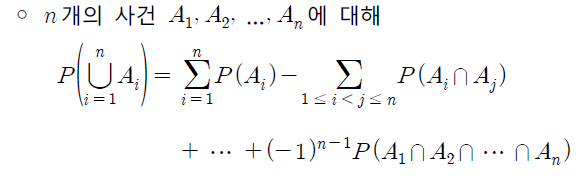
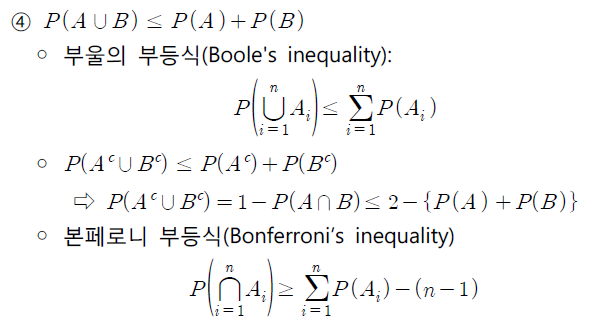
- 네 번째 성질은 P(A ∪ B) ≤ P(A) + P(B) 이다.
- 세 번째 성질에서 P(A ∩ B) 가 항상 0보다 크기 때문에 P(A ∪ B) ≤ P(A) + P(B) 가 성립된다.
- 네 번째 성질은 3개인 경우에도 마찬가지로 P(A ∪ B ∪ C) ≤ P(A) + P(B) + P(C)도 성립된다.
부울 부등식(Boole's inequality)
- 또한 네 번째 성질은 P(A^c ∪ B^c) ≤ P(A^c) + P(B^c)도 성립된다는 것을 의미한다.
- 여기에 드모르간 법칙을 적용하면,
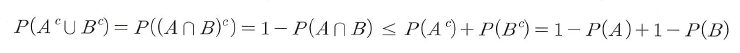
- 위와 같이 정리할 수 잇으며 최종적으로 아래와 같은 부등식을 얻을 수 있다.
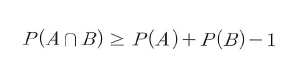
- 이에 대하여 수학적 귀납법을 이용하여 확률의 기본 성질 네 번째를 일반화 하면 n개에 사건에 대하여 아래 식이 나온다.
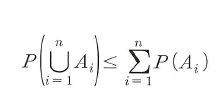
- 해당 부등식을 부울 부등식이라고 하며, 이 부등식을 이용하면 합사건에 대한 확률의 상한값을 얻을 수 있다.
본페로니 부등식(Bonferroni's inequality)
- 부울 부등식에서 A_i를 A_i^c로 대체하면 아래 식을 유도할 수 있다.
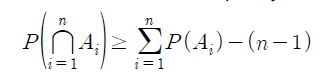
- 이 부등식을 본페로니 부등식이라고 하는데, 해당 부등식을 통해 교사건의 하한값을 얻을 수 있다. 추후 배울 분산분석에 이용된다.
요약
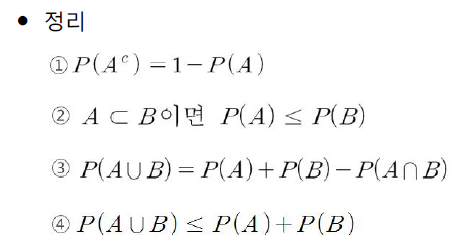
- 해당 확률의 기본적인 성질을 증명하는 과정을 배웠다.
- 그 중에서 1번과 3번은 매우 자주 사용하는 성질이다.
- 4번 성질에 의해서 P(A ∩ B) ≥ P(A) + P(B) -1이 유도되는 것도 알 수 있다.
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -3. 독립사건 (2) | 2024.01.29 |
|---|---|
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -2. 조건부 확률 (2) | 2024.01.22 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -4. 확률계산 실습(R) 및 퀴즈 (0) | 2024.01.21 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -3. 통계적 확률 (0) | 2024.01.20 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -2. 경우의 수 (0) | 2024.01.20 |




