공부하는 블로그
[통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -4. 확률계산 실습(R) 및 퀴즈 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
과제
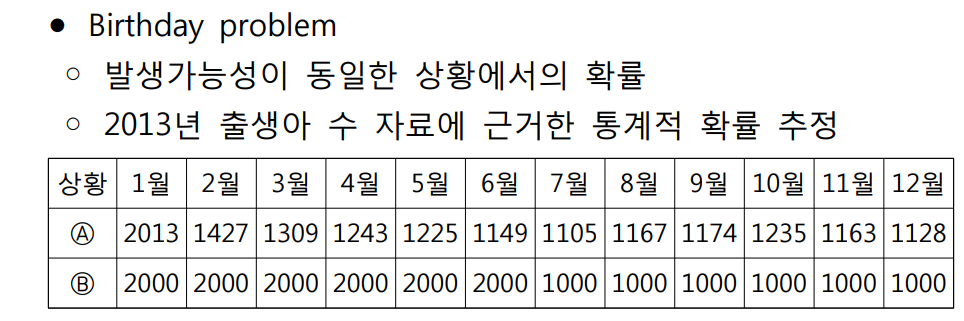
실습 내용 중 생일 문제에서 상황 A는 우리나라 2013년도 출생데이터를 가지고 했습니다.
그렇다면, 상황 B에서 k=5, 10, 25, 50, 100일 때 통계 확률을 추정해보시기 바랍니다.
그리고 반복수는 안정적인 결과를 위해서 10만 번을 반복해보세요.
daily <- scan()
2000 2000 2000 2000 2000 2000 1000 1000 1000 1000 1000 1000
# 해당되는 달에 몇 일이 있는지 표시한 것
monthday <- c(31,28,31,30,31,30,31,31,30,31,30,31)
# 반복해서 daily에 있는 값들을 month만큼 반복하라는 것.
births <- rep(daily,monthday)
birthprob <- births/sum(births)
# k=5,10,20,30,40,50일 때 100,000개 표본
n <- 365
nomembers <- c(5,10,20,30,40,50)
noSim <- 100000
for (k in nomembers){
result <- 0
for (i in 1:noSim)
{
x <- sample.int(n,k,replace=T,prob=birthprob)
result <- result + (length(unique(x)) == k)
}
cat(k,"명 선택할 때\n")
cat(" # of 생일이 모두 다른 경우:",result,"\n")
cat(" 생일이 모두 다를 확률:",result/noSim,"\n")
}

퀴즈
다음의 3가지 확률실험에 대하여 표본공간을 구해보세요.
1) 4개의 윷을 차례로 던지는데 엎어지는 것(R로 표시)이 나오면 던지는 것을 중단한다. 젖혀지는 것은 F로 표시
→ {R, FR, FFR, FFFR, FFFF}
2) A팀과 B팀이 3전 2선승제 경기를 한다. 각 경기에서 A팀이 이기면 A, B팀이 이기면 B로 표시하고 무승부는 없음
→ {AA, BB, ABA, ABB, BAA, BAB}
3) 실력이 비슷한 (a, b, c) 세 사람이 시험을 보는데 결과는 등수로 표시된다. 동점은 없음
→ {abc, acb, bac, bca, cab, cba}
※ 강좌는 청강한 것이라 과제 및 퀴즈 검토받지 못하였습니다. 학습한 내용 기반으로 작성한 것이므로 정답인지 아닌지 알 수 없습니다.
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -2. 조건부 확률 (2) | 2024.01.22 |
|---|---|
| [통계학의 이해Ⅰ] 6주차 조건부 확률 -1. 확률의 정리 (2) | 2024.01.22 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -3. 통계적 확률 (0) | 2024.01.20 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -2. 경우의 수 (0) | 2024.01.20 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -1. 확률이란? (0) | 2024.01.17 |




