공부하는 블로그
[통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -1. 확률이란? 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.
학습목표
- 확률을 정의하기 위한 전제 조건을 알아본다.
통계학이란?

- 통계학은 관심을 갖는 모집단이 있을 때 해당 모집단의 특성을 알아보기 위해 표본을 얻고, 이 표본의 특성을 이용하여 새로운 모집단을 만드는 과정이다.
- 그리고 모집단에서 표본을 어떻게 추출할 것인지에 대하여 조사, 실험, 관찰과 같은 방법들이 있다.
- 표본의 특징을 파악하기 위해 표, 그래프, 평균, 표준편차 등을 확인하는 방법이 있는데, 이를 기술통계라고 한다.
- 궁극적으로 관심을 갖는 것은 모집단이기 때문에 표본에서 얻어진 정보를 바탕으로 새로운 모집단을 생성하는 과정을 통계적 추론이라고 한다.
- 해당 과정이 잘 일어난다면 원래 모집단과 새로운 모집단은 유사할 것이고, 잘 일어나지 않는다면 두 모집단은 전혀 다른 모집단이 될 수 있다.
- 여기서 표본을 추출할 때, 언제 누가 어떻게 표본을 추출하는지에 따라 매번 표본이 달라질 수 있다.이를 설명하기 위해 확률을 배우게 되는 것이다.
- 표본의 성질이 매번 바뀌는지 바뀌지 않는지 확인하기 위해서는 모집단에 대해 알고 있어야 된다. 이를 통해 나온 결과값이 모집단과 얼마나 차이가 나는지, 어떤 변동성을 갖고 있는지 확인해볼 수 있다. 따라서 모집단에 대해서 알고 있다고 전제하고, 이 때 표본이 어떠한 성질을 갖고 있는지 알아보는 것이다.
확률(Probability)이란?
- 몇 가지 실험을 통해 확률이 발생하는 상황에서의 공통적인 특징을 확인한다.
- 주사위 던지기
- 앞면이 나올 때까지 동전 던지기
- 휴대전화의 수명
- 실험을 시행하기 전에 발생할 수 있는 모든 결과를 알 수 있다.
- {1, 2, 3, 4, 5, 6}
- 앞면을 H (head), 뒷면을 T(tail)라고 하면, {H, TH, TTH, ...}
- x를 수명(단위 일)이라고 하면, {x | 0 ≤ x}
- 실험을 하기 전까지 이들 결과 중 어떤 것이 발생할 것인지에 대해 확실하게 예측할 수 없다. → 불확실성
▶이 두 특징을 가지는 실험을 확률실험(random experiment)이라고 한다.
- 통계학에서는 확률 표현이 크게 세 가지로 나뉘게 된다.
- Probability: 항상 0~1 사이라는 개념이 들어간다.
- Random: 무작위다.
- Stochastic : 여기 과정에서는 다루지 않는다.
- 이 확률 실험에서 발생 가능한 모든 결과들을 모아 놓은 집합을 표본공간(sample space)라고 하는데, 표본공간 기호는 Ω라고 표기한다.
- 표본공간 내에서 관심을 가지는 부분집합을 사건(event)라고 한다. 예전에는 사상이라는 표현을 사용하기도 했다.
- 홀수가 나오는 경우, {1, 3, 5}
- 3번 이하로 던지는 경우, {H, TH, TTH}
- 10년 이상 사용하는 경우, {x ≥ 10}
- 확률을 얘기할 때에는 단순히 확률이 아니라 어떠한 사건이 일어날 확률이라고 얘기한다. 이 사건은 표본공간 내에 존재하는 것이고, 표본공간이 만들어지기 위해서는 확률실험을 해야된다. 따라서 확률실험으로부터 출발을 하게 된다.
▶확률 (Probability): 어떤 사건이 발생할 가능성이 얼마나 되는지를 나타내는 0과 1사이의 값으로 표현된 수치적 측도
- 0으로 갈수록 가능성은 작고 1로 갈수록 가능성은 커지는 것이다.
- 확률을 언급하기 위해서는 확률실험이 전제, 표본공간과 사건이 설정되어야 된다.
- 항상 확률실험이 전제가 되고 그에 따라 표본공간이 만들어지고 그 내의 부분집합인 사건의 확률로 언급하는 것이다.
- 표본공간과 사건 모두 집합이기 때문에 집합 관련 연산이나 정의에 대해 알 필요가 있다.

- 합사건; A와 B 둘 중 하나라도 들어간 것
- 교사건: A이고 B인 경우로 A도 포함 B도 포함되는 경우
- A의 여사건: A사건의 밖에 있는 것 중에서 표본공간 내에 있는 것

- 교환법칙: A와 B의 교(합)사건과 B와 A의 교(합)사건은 같다는 것
- 결합법칙: 총 3번 진행할 경우 앞을 먼저하는 것과 뒤를 먼저하는 것은 동일
- 분배법칙: A와 B의 합사건과 C의 교사건은 A와 C의 합사건을 구하고 B와 C의 합사건을 구한 뒤 그 둘의 교사건으로 묶은 형태로 표현 가능
- 드모르간법칙: A와 B의 합사건 전체의 여사건은 각각의 사건의 여사건의 교사건이 된다. (합의 반대가 교이다.) 마찬가지로 A와 B의 교사건 전체의 여사건은 각각의 여사건의 합사건으로 표현할 수 있음
- 무한개의 사건이 존재: 여러 사건이 있을 경우 전부 합사건으로 표현하기 보다는 간단하게 summation한 것처럼 i는 1부터 n까지 union하는 식으로 표현 가능, 반대로 intersection 1부터 n가지 표현 가능
- 배반사건 (disjoint, mutually exclusive): 임의의 두 사건 A와 B가 공통 부분이 없는 경우, 수식으로는 두 사건의 교집합이 공집합이다 라고 한다.
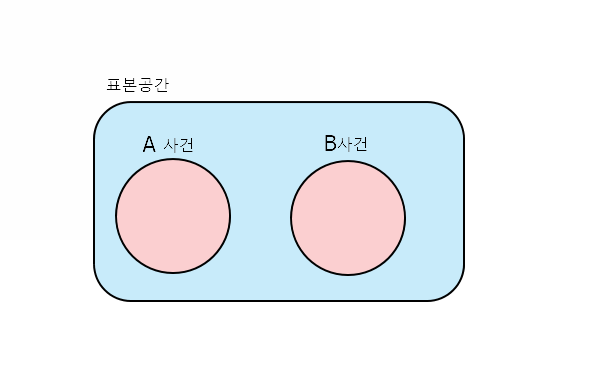
- 위처럼 집합 간의 관계를 이해하기 쉽게 보여주는 그림을 벤다이어그램(Veen diagram)이라고 한다.
에시

- 전체 표본공간 Ω는 위처럼 표현하며 총 16가지가 나온다.
- 관심있는 사건 A와 B는 위처럼 표현이 가능하다.
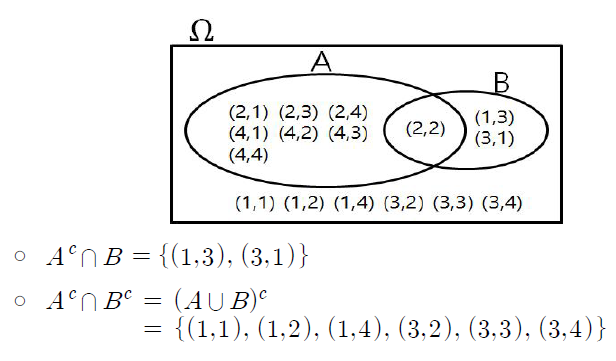
- 이를 벤다이어그램으로 표현하면 위 그림과 같이 나오고 각각의 사건에 대하여 눈으로 쉽게 알 수 있다.
고전적 확률 (Classical probability)
- 17세기 중반 도박 문제를 해결하기 위해 나온 예제이다.파스칼이나 페르마 등이 도박문제에 대해 의견을 교환하면서 확률을 수리적으로 다루기 시작하였다.
- 이들은 카드게임에서 각 패가 발생할 수 있는 빈도를 계산하고 빈도가 적은 패를 더 높은 패로 정했다.
- 그 당시 확률은 표본공간에서 사건에 해당되는 원소가 차지하는 비율로 정의하였다.
- 표본공간이 n개의 원소로 이루어져 있고 각 원소들의 발생가능성이 동일하다면 k개의 원소를 가지는 사건 A의 확률은 직관적으로 표본공간에서 A가 차지하는 비율이 될 것이다.
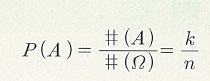
- #(A)와 #(Ω)은 각각 사건 A와 표본공간 Ω에 속한 원소의 개수
- 고전적확률은 각 원소의 발생가능성이 동일(equally likely)하다는 가정하에서 정의

- 예를들어 주사위를 던지면 모든 숫자의 발생 가능성은 동일하다고 볼 수 있음
- 이때 표본공간의 원소를 근원사건이라고 하며 근원사건의 발생가능성이 동일하다는 것은 equally likely라고 함
- P(A)는 probability of event A를 표현한 것으로 A사건이 발생할 확률이다.
- 주사위의 경우 간단하지만, 카드게임으로 가면 해당 문제가 매우 복잡해진다. 표본공간의 원소의 개수와 사건 A의 원소의 개수를 효율적으로 알 수 있는 방법을 정리한 것이 경우의 수(the number of cases)이다.

- 정사면체 주사위는 기본적으로 각 눈이 나올 가능성이 동일해서 고전적인 확률 상황에 맞음
- 사건 A와 B에 대하여 벤다이어그램을 통해 쉽게 원소의 개수를 파악할 수 있음
- P(A); 첫 번째 주사위가 짝수일 확률
- P(B): 두 주사위의 합이 4일 확률
- P(A^c ∩ B); 첫 번째 주사위가 홀수이고 두 주사위의 합이 4일 확률
- P(A^c ∩ B^c) ; 첫 번째 주사위가 홀수이고 두 주사위의 합이 4가 아닐 확률
연속표본공간(continuous sample space)
- 표본공간이 셀 수 없을 정도로 많은 원소로 이루여져 있는 것
- 연속표본공간에서는 표본공간뿐만 아니라 대부분의 사건도 무한개의 원소를 갖는다.
- 따라서 원소의 수를 비율로 표시하면 확률이 ∞/ ∞ 형태가 되기 때문에 정의하기 어려움
- 발생가능성이 동일한 상황을 선이나 평면 등을 이용
- 사건 A가 발생한다는 것은 Ω내에서 무작위로 한 점을 선택할 때, 이 점이 영역 A에 있다는 의미
- 사건 A의 확률은 전체 영역에서 A가 차지하는 비율이다.

예제
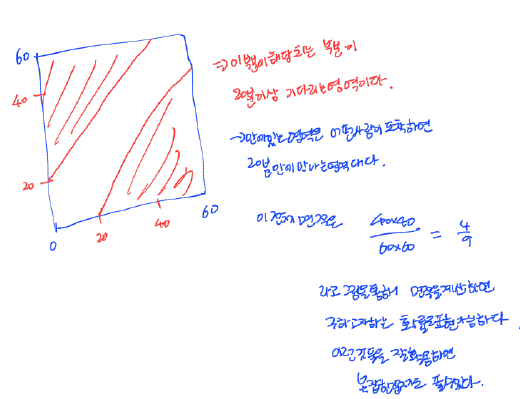
- 두 사람이 0시~1시 사이에 만나기로 함
- 각각의 사람은 0시~1시 사이에 무작위로 도착
- 먼저 도착한 사람이 다른 사람을 만날 때까지 20분이상 기다릴 확률?
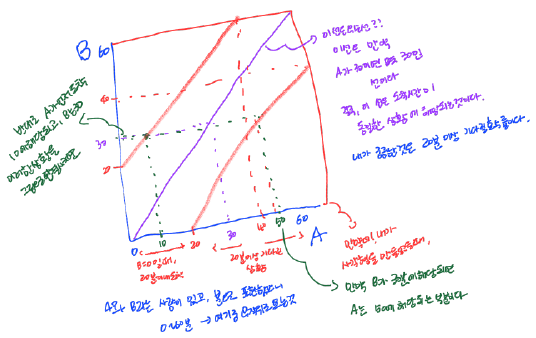
요약
- 표본공간은 발생가능한 것을 다 모아놓은 집합이다.
- 표본공간과 불확실성의 특징을 가진 경우를 확률실험이라고 한다.
- 확률은 어떠한 사건이 발생할 가능성을 0과 1사이로 표시한 것이다.
- 고전적인 확률에서는 발생가능성이 동일하다는 것이 전제가 되고 표본공간의 원소 개수에 대하여 A 사건의 원소 개수를 비율로 표시한 것이다.
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -3. 통계적 확률 (0) | 2024.01.20 |
|---|---|
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -2. 경우의 수 (0) | 2024.01.20 |
| [통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -4. 기술통계 실습 (R)-과제 (2) | 2024.01.15 |
| [통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -3. 공분산과 상관계수 (0) | 2024.01.15 |
| [통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -2. 비교그림과 산점도 (0) | 2024.01.15 |




