[통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -3. 공분산과 상관계수

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 두 수치자료의 직선관계의 정도를 나타내는 통계값을 알아본다.

---

공분산과 상관계수

• 산점도 : 두 수치변수 간에 관계가 잇는지를 시각적으로 확인
• 두 수치변수 간에 직선관계가 어느 정도인지를 나타내는 통계값
• 자료표시: 

통계학의 이해Ⅰ 강의 자료 4-3의 페이지1

통계학의 이해Ⅰ 강의 자료 4-3의 페이지2

• 왼쪽 그림은 양의 기울기를 갖는 선분을 중심으로 분포되어 있다.
• 오른쪽 그림은 음의 기울기를 갖는 선분을 중심으로 분포가 되어 있다.
• 해당 그림에서 x축 또는 y축의 값에 임의의 숫자를 더하거나 빼더라도 형태는 변하지 않는다. (평행이동해도 변화 x)
• 즉, 두 변수의 직선 관계는 위치에 영향을 받지 않는다.
• 따라서 직선관계를 나타내는 측도는 자료들의 위치에 영향을 받지 않아야 한다.
• 자료의 위치에 영향을 받지 않게 하는 방법은 각 자료의 중심위치인 값을 빼고 분석하는 것이며 여기서는 자료의 표본평균을 중심위치로 놓는다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지2

• 양의 기울기를 가지는 경우 (x bar, y bar) 표본 평균을 중심으로 1과 3사분면에 자료들이 많고 길게 분포된다.
• 음의 기울기를 가지는 경우 대부분 자료가 2와 4사분면에 길게 분포되어 있다.
• 따라서 자료의 직선관계를 표시하고자 할 때, 표본평균을 중심으로 1과3 그리고 2와 4사분면의 자료가 동일한 성질을 가지고 있다고 볼 수 있다.
• 양 끝 데이터가 직선관계를 잘 표현하며 서로 멀어질수록 직선관계를 잘 표현하는 것이다.
• 이러한 성질을 반영하여 변수의 편차를 곱하는 것이다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지3

• 변수의 편차를 곱하게 되면 1과 3사분면의 값은 양수, 2와 4사분면의 값은 음수로 표시된다.

표본공분산(sample covarianve)

통계학의 이해Ⅰ 강의 자료 4-3의 페이지4

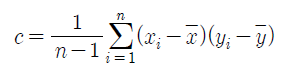
• 위의 왼쪽그림; 양의 기울기인 선분에 자료가 모여있음 → c > 0
• 위의 오른쪽 그림; 음의 기울기인 선분에 자료가 모여있음 → c < 0

통계학의 이해Ⅰ 강의 자료 4-3의 페이지4

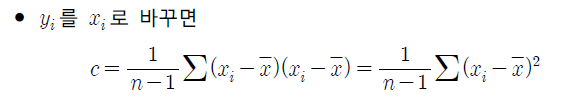
• 해당 식에 표본분산을 계산할 때처럼 자유도를 적용한 통계값을 생각할 수 있다. (표본의 개수로 보정하는 것)
• 표본분산의 식에서 x_i를 y_i로 바꾸면 C_xy가 된다. 이렇게 두 변수 x와 y의 분산형태를 가진다고 하여 통계값 C_xy를 표본공분산(sample covarianve)이라고 한다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지6

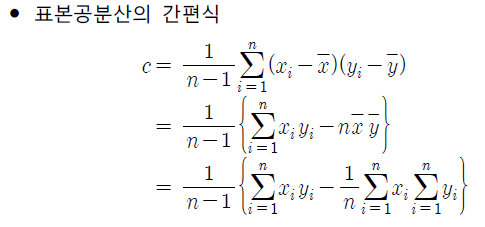
• 곱한 것의 합과 각각의 합이 있으면 쉽게 계산할 수 있다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지5

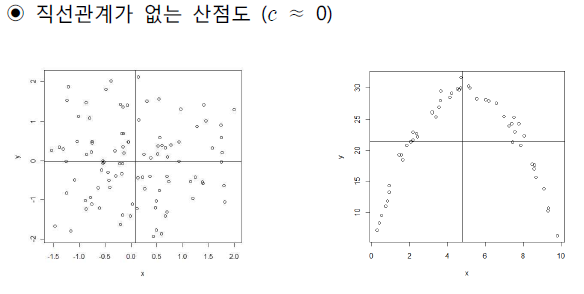
• 직선 형태가 없이 비슷한 패턴으로 분포되어 있는 경우 0에 가까운 값이 된다.
• 우측 그림과 같이 2차 곡선 관계가 있는 경우에도 1사분면의 값과 2사분면의 값이 상쇄되고, 3사분면의 값과 4사분면의 값이 상쇄되어 0에 가까워진다.
• 주의해야할 점은 직선관계를 나타내는 것이다. 0에 가깝다는 것은 직선관계가 보이지 않는 다는 것이지 어떠한 관계도 보이지 않는다는 것은 아니다.
• 하지만 공분산을 사용하는데 문제점은 측정 단위에 영향을 받기 때문에 그 값 자체로 선형관계 정도를 알 수 없다는 것이다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지7

통계학의 이해Ⅰ 강의 자료 4-3의 페이지8

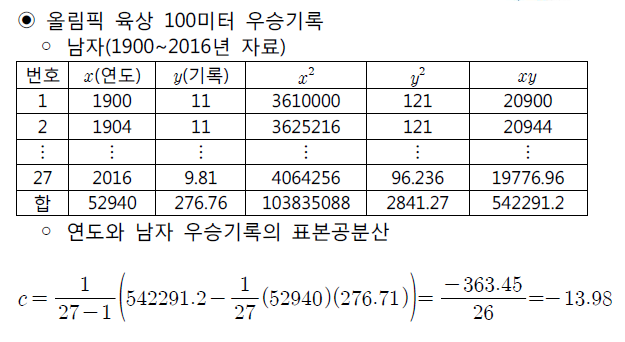
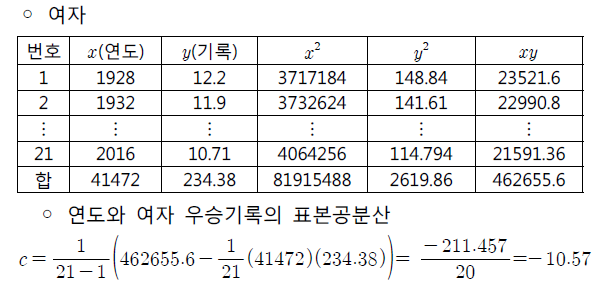
• 에시에서 초 단위로 표본공분산을 계산하였는데, 만약 분 단위로 표시하면 똑같은 자료이지만 초 단위 때보다 표본 공분산은 1/60의 값이 된다.
• 해당 문제를 해결하는 방법은 측정 단위에 영향을 받지 않게 자료를 표준화하여 표본공분산을 구하는 것이다.

표본상관계수(coefficient of correlation)

• 표본공분산의 문제점을 해결하기 위하여 자료를 표준화하여 구한 표본공분산
• 아래 식에서 S_x는 x의 표준편차, S_y는 y의 표준편차이다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지10

통계학의 이해Ⅰ 강의 자료 4-3의 페이지11

• 여기서 S_xx와 S_yy는 편차의 제곱합으로 수정제곱합(corrected sum of squares)라고 한다.
• 이러한 표본상관계수는 아래와 같은 성질을 갖는다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지12

통계학의 이해Ⅰ 강의 자료 4-3의 페이지13

상관관계 사용 시 주의할 점

• 두 변수 간에 직선관계가 있는지를 나타낼 뿐 인과관계를 나타내는 것은 아니다.
  • 예) 휴대전화 보급률과 기대수명에 대한 상관계수
    • 매우 높은 양의 상관관계를 가짐
      → 기대무셩을 늘리기 위해 휴대전화 보급을 늘려야 한다? 비상식적인 결론 도출
    • 높은 양의 상관관계를 가지는 이유는 시간에 따라 지속적으로 증가하는 자료들이기 때문이다.
• 이처럼 두 변수에 공통적으로 영향을 주거나 관계가 있는 변수를 "잠복변수(lurking variable)"라고 한다.
  • 연도에 따라 보급률 증가, 기대수명 증가
• 이처럼 제 3의 변수에 의해 나타나는 상관관계를 "허위상관(squrious correlation) "또는 "가짜상관"이라고 한다.
  • 허위상관은 잠복변수에 의해서 발생할 수 있다.
  • 보급률과 기대수명에서 연도의 영향력을 제거하고 상관관계를 유도해야된다.

통계학의 이해Ⅰ 강의 자료 4-3의 페이지15

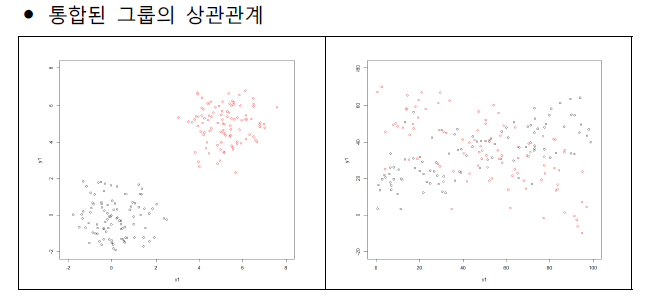
• 왼쪽 그림의 경우 두 개의 다른 그룹인데 구분하지 않고 함께 분석한다면 1과 3사분면에 위치하여 공분산이 높게 나올 수 있다.
• 오른쪽 그림의 경우 전체적으로는 관련이 없어 보이는데, 그룹을 나누어 보면 빨간색 점들과 검정색 점들이 각각 상관관계가 있다. 
• 따라서 분석을 할 때에는 실제로 그룹이 나누는지도 잘 파악해야된다.

---

요약

• 직선관계의 정도는 표본공분산과 표본상관계수를 통해 알 수 있다.
• 표본공분산은 측정 단위의 영향을 받기 때문에 그 값 자체로 선형관계 정도를 알 수 없다.
• 따라서 표준화된 자료의 표본공분산인 표본상관계수를 통해 선형관계 정도를 알 수 있다.
• r이 1에 가까울수록 높은 상관관계를 갖는다.
• r이 0에 가까우면 직선관계가 없을 뿐 아무런 관계가 없는 것은 아니다.
• 상관관계를 분석할 때 허위상관과 통합된 그룹의 상관관계는 주의해야된다.