공부하는 블로그
[통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -1. 분할표와 그래프 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.
학습목표
- 다변량 범주형 자료를 표나 그래프를 이용하여 정리하는 방법을 알아본다.
변수(자료) 형태

- 1번일 경우 비교를 하는데, x에 따라 y의 빈도 또는 비율에 차이가 있는지 확인할 수 있다.
- 2번일 경우 비교에 목적을 두고 x 에 따라 평균이나 분산에 차이가 있는지 확인할 수 있다.
- 2번과 3번은 또한 분류에 목적을 두고 분석할 수 있다.
- 4번의 경우 관계를 확인하기 위한 목적을 두고 x와 y의 수치적 관계를 확인할 수 있다.
- 분석목적
- 비교: X에 따라 Y에 차이가 있는가?
- 관계: X와 Y가 관련이 있는가? X가 Y에 영향을 주는가?
- 분류: X에 따라 Y를 분류할 수 있는가? X,Y가 비슷한 것끼리 묶을 수 있는가?
- 이처럼 다변량 자료일 경우 변수의 형태와 분석 목적에 따라 분석하는 방법이 달라진다.
분할표(cotingency table)
- 두 개 이상의 변수를 동시에 고려하여 각각의 범주에 관측개체의 빈도를 정리한 교차표(cross tabulation)

- 칸(cell): 각 범주에 교차되는 부분
- 행과 열의 범주 수를 같이 표시하여 위와 같은 표를 2x4 분할표라고 한다.
- 분할표에도 비율을 표시할 수 있는데, 비율을 표시할 때에는 분석 목적 또는 자료를 어떻게 수집했는가에 따라 다르게 표시된다.
분할표 예시
- 세 가지 스마트폰 모델에 대한 남녀별로 선호도 비교
- 남자 76명과 여자 70명을 대상으로 세 가지 모델(A, B, C) 중 가장 마음에 다는 모델을 선택


비율(상대도수)표시
- 분모
- 성별 합계 (76, 70)
- 스마트폰 모델별 합계 (56, 56, 38)
- 전체 합 (146)
- 비율은 분석 목적 또는 자료가 어떻게 수집되었는지에 따라 다르게 표시
- 분석 목적은 선호도에서 남녀 간 차이 여부
- 따라서 남자 중 각각의 모델을 선호한 비율과 여자 중 각각의 모델을 선호한 비율을 비교해야된다.

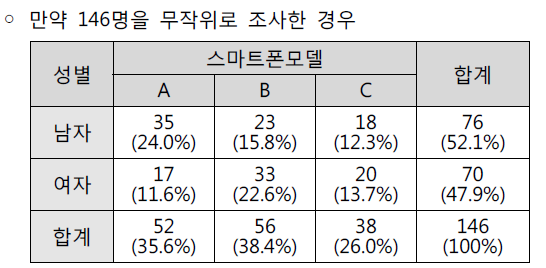
- 성별에 따른 선호도 차이를 조사하는 것이 아닌, 146명을 무작위로 조사한 경우 146을 기준으로 비율을 표시해야된다.
수치자료의 분할표
- 수치자료를 범주화하고 분할표를 작성한다.
- 부자의 신장: 165, 170, 175, 180을 기준으로 범주화
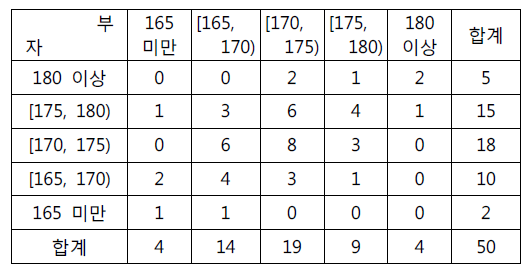
- 순서자료의 크기 순서대로 밑에서 위로, 왼쪽에서 오른쪽으로 갈수록 커지게 표시를 해주면 2차원 그래프 x, y축과 동일한 형태로 그릴 수 있기 때문에 대략적인 관계도 확인이 가능하다.
- 해당 자료에서는 아버지가 크면 아들이 큰 경향이 있다는 것을 표이지만 시각적으로 확인 가능하다.
k차원 분할표(k-dimensional contingency table)
- 3개 이상의 범주형 변수에 대해서도 분할표를 작성할 수 있는데, 변수의 개수가 k라고 하면 k원 분할표(k-way contingency table) 혹은 k차원 분할표라고 부른다.
- 타이타닉(RMS Titanic)호 생존자와 사망자수
- 변수: 생존여부 (생존, 사망), 성별(남, 여, 어린이), 객실등급 (1, 2, 3, 승무원)
- 타이타닉(RMS Titanic)호 생존자와 사망자수
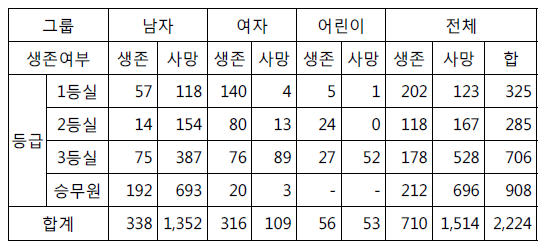
- 총 24개의 칸에 대한 3차원 분할표가 생성된다.
- 생존율
- 객실 등급에 따른 생존율: 1등실 - 62.2%, 2등실 - 41.4$, 3등실 - 25.2%, 승무원 - 23.3%, 전체 31.9%
- 성별에 따른 생존율: 20.0%, 74.4%, 51.4%
그래프를 이용한 자료 정리
원도표(pie chart)
- 비교 그룹별로 파이차트 작성 (스마트폰 선호도 예시)
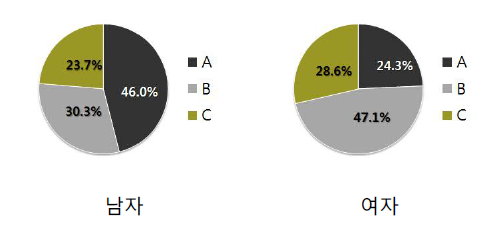
- 전체가 100이 되도록 남녀별로 구분해서 상대적으로 얼마나 차지하는지 볼 수 있음
막대그래프(Bar chart)
- 분석 목적과 자료 형태에 맞게 빈도/비율 중 선택
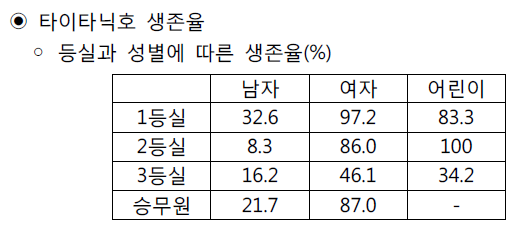
- 등실과 성별을 따로 분류해서 비교하는 것이다.
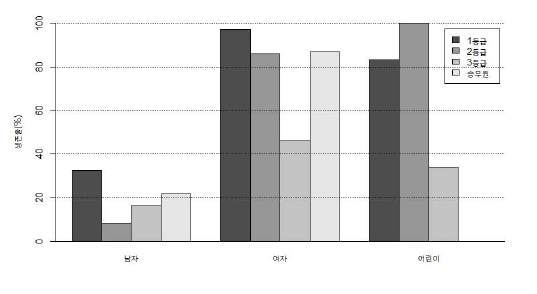
- 전체적으로 승무원의 생존율이 낮았지만 남자들끼리, 여자들끼리 분류해서 비교하면 승무원은 높은 편이다.
- 남자들 중에서 승무원의 생존율은 2번째로 높고, 여자들끼리 봐도 승무원이 2번째로 높다.
- 남녀로 구분했을 때 승무원의 생존율은 1등실을 제외한 나머지 등실의 승객보다 생존율이 높다.
- 남성의 비율을 확인해보면 1등실 - 54.9%, 2등실 - 64.4%, 3등실 73.7%, 승무원 97.5%
- 따라서 승무원의 대부분이 남자였고, 남자들은 전체적으로 생존율이 낮기 때문에 해당 결과가 나온 것이다.
- 승무원의 생존율이 낮다 라고 보기에는 무리가 있다.
- 이처럼 전체 자료를 분석한 결과와 세부적으로 분석한 결과가 상반되게 나오는데, 이를 심슨의 패러독스라고 하고 이러한 현상이 많이 발생한다.
- 따라서 정확하게 파악하기 위해서는 자료를 세분화해서 볼 필요가 있다.
- 결론이 달라질 수 있기 때문에 자료를 크게만 보는 것이 아니라 세분화하여 분석해야된다.
요약
- 분할표는 비율을 어떻게 표시하냐에 따라서 해석이 달라질 수 있다.
- 분류 변수에 따라 원도표와 막대그래프를 그릴 수 있다.
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -3. 공분산과 상관계수 (0) | 2024.01.15 |
|---|---|
| [통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -2. 비교그림과 산점도 (0) | 2024.01.15 |
| [통계학의 이해Ⅰ] 3주차 일변량 자료에 대한 수치적 기술통계 -6. 기술통계 실습 (R)-과제 (0) | 2024.01.14 |
| [통계학의 이해Ⅰ] 3주차 일변량 자료에 대한 수치적 기술통계 -5. 수치자료의 형태 (0) | 2024.01.14 |
| [통계학의 이해Ⅰ] 3주차 일변량 자료에 대한 수치적 기술통계 -4. 수치자료 분포의 산포2 (2) | 2024.01.14 |




