[통계학의 이해Ⅰ] 3주차 일변량 자료에 대한 수치적 기술통계 -4. 수치자료 분포의 산포2

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 자료들 간의 거리를 이용하여 산포도를 계산하는 방법을 알아본다.

---

표본분산과 표준편차

• 모든 자료들 간의 거리의 합을 이용하는 방법은?
• 거리(distance): 임의의 점 a, b, c에 대해 아래 성질을 만족한다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지1

• 해당 거리를 이용하여 자료들 간의 퍼져있는 정도를 알 수 있다.
• 이러한 성질을 만족하는 D는 수없이 많은데 그 중 우리는 D(a, b) = |a - b|와 D(a, b) = (a - b)^2에 관심을 갖는다.
• 이들 거리를 이용하면 모든 관측개체들 간 거리의 합을 다음과 같이 계산할 수 있다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지2

• 자료들이 넓게 퍼져 있으면 이 합들은 커질 것이고 모여 있으면 작아진다.
  • 위의 측도를 사용하기 위해서는 n^2개의 거리 합을 계산해야 하므로 n이 커지면 계산의 부담이 생길 수 있다.
  • 따라서 중심위치 a에서 자료들이 떨어져 있는 거리의 합을 생각해 볼 수 있다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지2

• 그렇다면 해당 적절한 중심위치인 a를 어떻게 선택해야 할까?
• a가 좋은 중심위치가 되려면 자료들 간 거리가 가능한 짧아야함 →  거리의 합을 최소로 만드는 값 (자료들을 가장 잘 대표할 수 있는 중심위치이다.)

통계학의 이해Ⅰ 강의 자료 3-4의 페이지3

• L2( a )에서는 중심위치로 표본평균 x bar가 적절하다는 것을 알 수 있다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지4

• L1( a )의 경우 a 로 미분할 수 없으므로 위 그림을 통해서 이해할 수 있다.
• 왼쪽 그림에서는 자료가 2개 있을 때 a가 β처럼 자료들 사이에 있는 경우와 α 처럼 밖에 있는 경우를 생각해 볼 수 있다.
• α가 중심위치인 경우 모든 거리의 합은 β거리의 합 + 2k 가 된다.
  • 따라서 중심위치가 β일 경우가 α일때보다 더 적다는 것을 알 수 있다.
  • 표본 크기가 짝수이면 a가 중간에 있는 두 값의 사이에 있어야 L1(a)가 최소가 된다.
• 오른쪽 그림처럼 표본 크기가 3개일 경우에는 a가 β처럼 자료 중 가운데 값일 수 있고, α처럼 값들 사이에 있을 수 있다.
• α가 중심위치인 경우 모든 거리의 합은 β거리의 합 + k 가 된다.
  • 따라서 중심위치가 β일 경우 최소가 된다는 것을 알 수 있다.
• 결론적으로 L1(a)를 최소로 만드는 a는 표본중앙값 x tilda가 된다.
• 여기서 중요한 것은 어떤 거리를 사용하느가에 따라 적절한 중심위치가 달라질 수 있다는 것이다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지5

 

• 해당 기준들로 산포를 구하면 개수가 많아질수록 양수 값이 더해지니 커질수밖에 없다. 따라서 표본의 크기로 보정을 해줘야된다.
• 이렇게 보정해주는 것을 표본분산이라고 한다.

표본분산(sample variance)

통계학의 이해Ⅰ 강의 자료 3-4의 페이지6

 

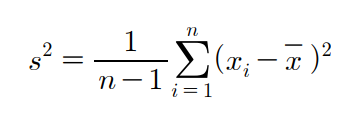
• 표본분산은 n개의 편차를 사용하는 것 같지만 "편차의 합은 0"이라는 제약조건 때문에 n-1개의 편차만 자유롭게 값을 가질 수 있다.
• 마지막 1개는 편차의 합이 0이 되도록 만드는 역할만 한다.
• 실제로 사용하는 것은 n-1개의 편차 정보를 이용하기 대문에 n이 아닌 n-1로 나누게 된다.
• 이러한 n-1을 자유롭게 가질 수 있는 편차의 개수라고 하여 자유도(degree of freedom)라고 한다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지7

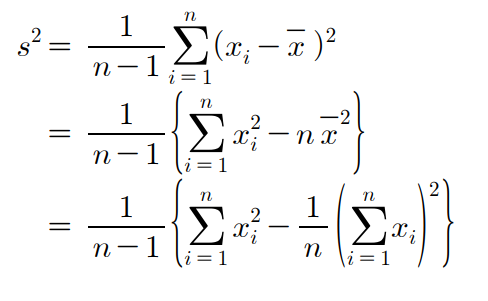
• 표본분산 수식을 전개시켜 좀 더 간단하게 계산할 수 있다.

표본표준편차(sample standars deviation)

• 표본분산은 편차의 제곱합을 이용하기 때문에 분산의 단위는 관측값 단위의 제곱이다.
• 눈으로 이해하는 산포와 일치하기 위해서는 자료를 측정할 때의 단위로 표시해야된다.
• 따라서 원의 거리를 계산할 때 처럼 표본분산을 제곱근을 취해 구할 수 있다. 
• 표본분산의 제곱근은 관측값과 동일한 단위로 퍼짐의 측도가 되며 이를 표본표준편차라고 한다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지8

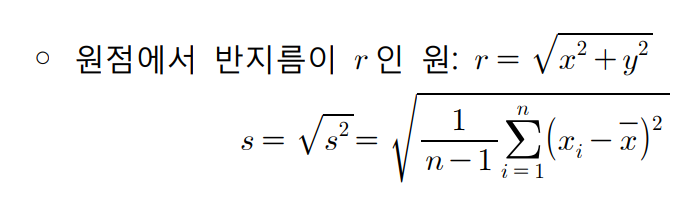
표준화(standardization)

• 표준화는 데이터들의 척도나 위치에 영향을 받지않도록 바꾸어주는 역할을 한다.
• 수능시험은 과목별로 난이도가 다를 수 있기 때문에 원점수로 과목 간 성적을 비교하면 문제가 있을 수 있다.
  • 따라서 원점수에 평균을 빼고 표준편차를 나누어 점수를 표준화하여 상대비교를 한다. (표준화점수 사용)

통계학의 이해Ⅰ 강의 자료 3-4의 페이지9

통계학의 이해Ⅰ 강의 자료 3-4의 페이지10

• 표준화는 평균이 0, 표준편차가 1이 되도록 만든다.
• 따라서 측정 단위에 영향을 받지 않게 중심위치와 척도(scale)를 조정해 절대비교가 가능하다.

변동계수(coefficient of variation)

• 표준편차가 평균에 영향을 받는 경우
  • 예) 다이어트 목표: 체중 100kg인 사람이 10kg (10%) 감량과 50kg인 사람이 10kg(20%)감량
  • (10kg, 10kg) 감량 vs (10%, 20%) 감량
• 표준편차만 이용하여 산포를 비교하는 것은 적절하지 않을 수 있어 평균으로 표준편차를 보정한 것이 변동계수이다.
• 100을 곱해 표본평균에 비해 표본표준편차가 얼마나 큰지 %개념으로 표시하기도 한다.
• 변동계수는 신장과 체중과 같이 단위가 전혀 다른 자료들의 퍼져있는 정도를 비교할 때에도 사용된다.

통계학의 이해Ⅰ 강의 자료 3-4의 페이지13

---

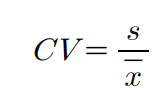
요약

• 분산은 자유도를 갖는 n-1개의 자료들을 이용한다.
• 표준화를 하면 평균은 0, 표준편차는 1이되어 다른 지표들 간 상대적인 비교가 가능하게 된다.
• 표준편차만 이용하여 산포를 비교하는 것은 적절하지 않을 수 있기 때문에 변동계수를 이용한다.