공부하는 블로그
[통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -2. 경우의 수 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.
학습목표
- 표본공간 및 사건의 원소 개수를 효율적으로 계산하는 기본 공식을 소개한다.
경우의 수(the number of cases)
- 확률을 계산하기 위해서는 표본공간과 사건에 있는 원소의 개수를 효율적으로 계산하는 것이 중요
- 연속적으로 이루어진 어떤 실험을 했을 때 몇 개가 나오는 것을 계산할 때 기본 법칙은 곱의 법칙(multiplication rule)
- 어떤 실험이 m개의 연속된 단계로 이루어짐
- n_i번째 단계에서 발생 가능한 결과의 수
- 전체 실험에서 발생 가능한 경우의 수

에제
- 세트메뉴의 경우의 수
- 세트메뉴에는 4가지 음료수, 2가지 샐러드, 5가지 메인, 4가지의 디저트 중에서 각각 하나씩을 선택
- 각각 발생 가능한 경우가 있고, 이를 전부 곱하면 경우의 수다.
- 선택할 수 있는 세트의 종류: 4 x 2 x 5 x 4 = 160
- 일반적인 문제: 1번부터 n번까지 적혀있는 공이 들어 있는 주머니에서 k개를 무작위로 선택
- 추출방법:
- 복원(with replacement)추출 : 주머니에서 공을 꺼낸 뒤 다시 넣고 뽑는 것
- 비복원(without replacement)추출: 주머니에서 공을 꺼낸 뒤 다시 넣지 않는 것 (한번에 뽑은 것 해당됨)
- 복원추출의 경우 매번 선택할 수 있는 것은 n개가 되지만, 비복원의 경우 뽑힌 개수만큼 줄어든 것에서 선택
- 뽑힌 순서:
- 순서 고려 O: (1, 2)와 (2, 1)은 다른 것 → 두 개
- 순서 고려 X: (1, 2)와 (2, 1)은 같은 것 → 한 개 (정렬한 것이 해당됨)
- 추출방법:

- 기존에 알고 있던 순열과 조합은 비복원이고, 복원을 하게 되는 경우 중복이 되는 것이다.
- (A) 중복순열 : 복원 + 순서 고려
- (B) 순열(permutation) : 비복원 + 순서 고려 [nPk]
- (C) 중복조합: 복원 + 순서 무시
- (D) 조합(combination): 비복원 + 순서 무시

중복순열
- 중복순열의 경우 매번 n개를 선택할 수 있으므로
- n x n x ... x n = n^k
순열
- 순열의 경우 비복원이기 때문에 뽑을 때마다 1개씩 줄어든다.
- n x (n-1) x (n-2) x ... x (n-k+1)
- 해당 식에 분모와 분자에 똑같이 (n-k) x ... x 1 을 곱해주면 분자는 n! 분모는 (n-k)!이 된다.
- 따라서, n!/(n-k)! = nPk 로도 표현 가능
예제
Birthday problem
- 1년을 365일이라고 할 때, k명이 가질 수 있는 생일의 경우의 수
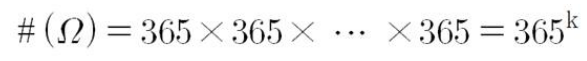
- A: k명의 사람이 모두 다른 생일을 가지는 사건
- 1~365 숫자 중 k개를 비복원 추출 하는 것


- 사건 A가 발생할 확률 = A사건 원소의 개수 / 표본공간 원소의 개수이다.
- 이를 k에 따라서 계산을 해본 것으로 30명만 되어도 30%이하로 떨어진다.
조합
- 비복원 추출에서 순서를 고려한 것이 순열이고, 순서를 고려하지 않는 것이 조합이다.
- 조합을 고려하기 위해서는 순열을 고려해야 된다.
- 순열을 비복원 추출로 k개를 뽑고, 순서를 고려하는 단계로 나누어서 생각해보자.
- 따라서 순서를 고려한 순열에서 순서를 고려하는 단계를 나누면 순서를 고려하지 않는 비복원 추출인 조합이 되는 것이다.
- 만약 1,2,3이라는 k를 뽑고 순서를 지정하자고 한다면, 첫 번째 자리에 올 수 있는 것은 3, 그 다음은 2, 그 다음은 1이된다. 그렇게 되면 k개에 대하여 순서를 고려하는 경우의 수는 k!이다.
- 즉 순열에서 k!를 나누면 조합이 되는 것이다.
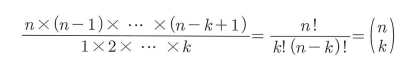
예제

- 순열로 1234에서 3개를 비복원 추출하는 경우의 수는 24개인데, 그림에서 묶은 단위들은 순서를 고려하지 않는다면 (sorting 한다면) 각각의 6개(3!)이 1개의 경우의 수로 변경이 되는 것이다.
- 따라서 1234에서 3개를 비복원 추출하고 정렬한 경우의 수는 24 / 3! = 4개이다.
중복조합
- 위 조합을 계산한 방법처럼 중복조합도 중복 순열에서 순서를 고려한 경우를 나누면 될까?
- 그렇게 되면 n^k/k!이어야 되는데 해당 식은 틀린 식이다.
- 아래 예를 통해 중복조합에 대하여 확인

- 보이는 것 처럼 중복조합은 실제로 1234에서 2개를 복원추출하고 정렬을 했을 경우 총 10가지 경우가 나온다.
- 중복순열은 4^2으로 총 16가지가 나오는데 여기에는 (1,1), (2,2), (3,3)이 정렬 전에는 하나이다.
- 하지만 중복조합을 생각하기 위해서는 앞에 추출한 1과 뒤에 추출한 1을 다르게 생각하고, 정렬전 (순서를 고려한 경우)을 그림처럼 구분하여 2개의 경우로 생각해야된다.
- 그렇게 되면 각각 순서 바뀐 것은 2배가 되고 20 / 2! = 10 으로 중복조합의 수가 되는 것이다.
일반식 유도

요약
- 공을 추출할 경우 추출방법과 배열 순서에 따라 4가지를 고려할 수 있다.
- 일반적으로 우리가 알고 있는 순열과 조합은 비복원이다. (한번에 추출한다.)
- 복원 추출을 하는 경우는 중복이 붙으면서 각각 중복순열과 중복조합이 되는 것이다.
- 순열과 중복순열은 순서를 고려한다.
- 조합과 중복조합은 순서를 고려하지 않는다.(정렬을 한다.)
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -4. 확률계산 실습(R) 및 퀴즈 (0) | 2024.01.21 |
|---|---|
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -3. 통계적 확률 (0) | 2024.01.20 |
| [통계학의 이해Ⅰ] 5주차 확률의 기본 개념과 원리 -1. 확률이란? (0) | 2024.01.17 |
| [통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -4. 기술통계 실습 (R)-과제 (2) | 2024.01.15 |
| [통계학의 이해Ⅰ] 4주차 다변량 자료 기술통계 -3. 공분산과 상관계수 (0) | 2024.01.15 |




