[통계학의 이해Ⅰ] 8주차 확률벡터 -2. 결합분포와 주변분포

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 두 확률변수의 확률구조를 설명하기 위한 결합분포와 주변분포에 대해 알아본다.
• 결합분포와 주변분포의 관계로부터 두 확률변수가 독립인지 아닌지를 확인하는 방법을 알아본다.

---

결합분포와 주변분포

• 여러 가지 변수의 자료를 얻고 이들 변수 간에 어떤 관계가 있는지에 관심을 가질 수 있다.
• 여러 가지 확률변수를 순서열(X1, X2, ..., Xp)로 표시한 것을 확률벡터(random vector)라고 한다.

동전 세 번 던지기

통계학의 이해Ⅰ 강의 자료 8-2의 페이지1

통계학의 이해Ⅰ 강의 자료 8-2의 페이지2

결합분포(joint distribution)

• 두 개 이상의 확률변수를 동시에 고려한 확률분포
• 두 확률변수의 결합분포를 이변량 분포(bivariate distribution)이라고 하며, p -개의 확률변수로 이루어진 확률벡터의 결합분포를 p-차원 다변량 분포(p-dimensional multivariate distribution)이라고 한다.
• 두 이산확률변수 X와 Y에 대해
  • f(x, y) = P(X = x, Y=y)
  • f(x, y): 결합확률질량함수(joint probability mass function)
  • 콤마(,)는 집합에서 ∩를 의미한다.

통계학의 이해Ⅰ 강의 자료 8-2의 페이지3

• 확률변수가 여러 개인 경우 X1 = x1, X2 = x2, ... Xn = xn인 형태이다.

동전 세 번 던지기

통계학의 이해Ⅰ 강의 자료 8-2의 페이지4

• 각각 table에 x = 1, y = 1일 때처럼 모든 x와 y에 대하여 개수를 세는 것이다.(전체 8개 중에서 몇 개 있는지)
• 이렇게 표현한 것이 결합분포이다.
• 여기서 알 수 있는 결합분포의 특징이 있다.
  • 모든 x, y에 대하여 f(x, y)는 0과 1사이의 값으로 표현된다.
  • f(x, y)를 모두 더하면 1이된다.
  • 확률분포의 성질 그대로 결합분포에도 해당 성질들이 만족한다.

결합확률밀도함수

• 두 연속확률변수 X와 Y에 대해, 결합확률밀도함수 f(x, y)는 x, y에서의 밀도를 나타내며 아래 성질을 만족

통계학의 이해Ⅰ 강의 자료 8-2의 페이지5

• 결합확률밀도함수 f(x, y)는 (x, y)에서 밀도가 상대적으로 얼마나 높은지를 나타내는 것
• 밀도가 마이너스인 경우가 없기 때문에 항상 0보다 크거나 같으며 상한은 없다.
• 이것들을 전부 누적시켜 더한 전체 부피는 1이다.

통계학의 이해Ⅰ 강의 자료 8-2의 페이지5

• X와 Y가 균일확률인 경우 전체 부피가 1이기 때문에 높이는 1/uv이다.

주변분포(marginal distribution)

통계학의 이해Ⅰ 강의 자료 8-2의 페이지6

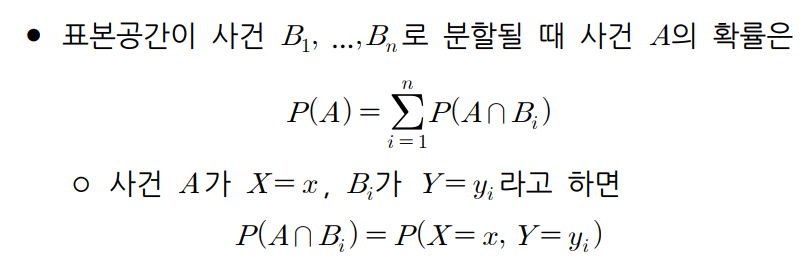
• 분할은 표본공간이 오버랩하지 않게 배반사건으로 나뉜 것이고, 다 합한 합집합이 표본공간이 되는 것이다.
• Y가 가질 수 있는 값이 y1, ..., yn이라고 할 때, X = x를 사건 A, Y = yi를 사건 Bi라고 하면 P(A ∩ Bi) = P(X = x, Y = yi)이며, 아래와 같은 식이 성립한다.

통계학의 이해Ⅰ 강의 자료 8-2의 페이지7

• 두 이산확률변수 X와 Y의 결합확률질량함수가 f(x, y)일 때, X의 확률질량함수는 모든 y의 결합확률질량함수를 더해 구할 수 있으며 반대로 Y의 확률질량함수는 모든 x의 결합확률질량함수를 더해 구할 수 있다.
• 이 경우 fX(x)를 X의 주변확률질량함수(marginal density function)라고 한다.
  • fX(x) : X의 주변확률질량함수
  • fY(y) : Y의 주변확률질량함수

통계학의 이해Ⅰ 강의 자료 8-2의 페이지7

• 연속형 확률변수에 대해서는 ∑를 ∫로 변경해주면 된다.

동전 세 번 던지기

통계학의 이해Ⅰ 강의 자료 8-2의 페이지8

• 각각의 주변확률질량함수를 다 더하여 구할 수 있다.

통계학의 이해Ⅰ 강의 자료 8-2의 페이지8

• 주변확률밀도함수에 대해서도 마찬가지로 구해줄 수 있다.

독립확률변수

• 이전에 두 사건 A와 B의 독립성에 대한 필요충분조건이 P(A ∩ B) = P(A)P(B) 였다.
• 여기서는 두 확률변수의 독립에 대해 논한다.
• 두 확률변수가 독립이라면 한 확률변수가 어떤 값을 갖더라도 다른 변수의 확률에 영향을 주지 않는다는 것의 의미한다.
• 이를 식으로 표현하면, 두 확률변수 X와 Y가 모든 x, y에 대하여 결합확률질량(밀도)함수가 주변확률질량(밀도)함수의 곱으로 표시할 수 있으며 이런 경우 X와 Y는 독립(independent)이라 한다.

통계학의 이해Ⅰ 강의 자료 8-2의 페이지9

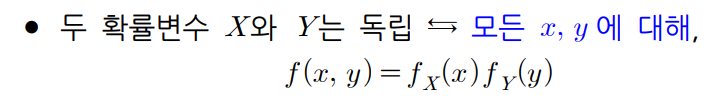
• 두 확률변수 X와 Y가 독립이면 두 결합확률함수가 각각의 주변확률함수의 곱으로 표시되고 확률변수가 가질 수 있는 값들이 서로 영향을 주지 않는다.

통계학의 이해Ⅰ 강의 자료 8-2의 페이지9

• 여러 확률변수에 대해서도, 결합분포가 각각의 주변 분포들의 곱으로 표시되는 경우 독립이다.(이산형과 연속형 모두)

동전 세 번 던지기

통계학의 이해Ⅰ 강의 자료 8-2의 페이지10

• fX(1) = 3/8, fY(1) = 3/4이므로 곱으로 표현이 되지 않기 때문에 X와 Y는 독립이 아니다.

통계학의 이해Ⅰ 강의 자료 8-2의 페이지11

• 또 다른 예제 위와같은 case에서는 모든 x, y에 대해 f(x, y) = fX(x)fY(y)가 성립한다.따라서 해당 경우 X와 Y는 서로 독립이다.
• 따라서 f(x, y) = g(x)h(y)처럼 곱의 형태로 표기가 가능하고 x와 y의 값이 별개인 경우(서로의 영향 x) 독립이라고 할 수 있다.

• • 로 표시되는 것들은 원리를 이용하여 쉽게 계산 가능하다.

---

요약

통계학의 이해Ⅰ 강의 자료 8-2의 페이지12

• X와 Y에 대한 결합확률질량함수는 항상 0과 1사이에 값에 존재하며, 다 더하면 총합이 1이다.
• 주변확률질량함수는 x를 구하고자 할 때는 y에 대한 값을 모두 더하고, y에 대해 구하고 싶을 때에는 x에 대해 모두 더하면 된다.
• 두 확률변수 X와 Y에 대해서 모든 x, y에 대해 f(x, y) = fX(x)fY(y)가 성립되면 독립이다.
  • 모든 결합분포가 주변분포들의 곱으로 표기