공부하는 블로그
[통계학의 이해Ⅰ] 8주차 확률벡터 -1. 분산과 표준편차 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.
학습목표
- 모집단의 분포가 얼마나 퍼져있는지를 나타내는 분산 및 표준편차의 계산과 성질에 대해 알아본다.
모분산(population variance)
- 표본평균은 자료의 중심위치이며 자료가 얼마나 퍼져있는가에 대한 대표적인 통계값은 분산 또는 표준편차
- 표본분산
- 표본크기: n
- 표본이 가질 수 있는 값 {x1, x2, ..., xn}
- ni: 표본 중 xi값을 가지는 표본의 수

- 표본분산을 구하는 식에서 모분산을 유도할 수 있다.
- 통계적 확률의 관점에서 볼 때, n을 계속 크게하면 표본분산은 모분산(population variance)이 될 것이다.
- 이 때, pi는 f(xi)[확률]로, xbar는 μ(모평균)로, n/(n-1)은 1로 수렴하게 되면서 표본분산이 모분산이 된다.
- 모분산은 σ^2로 표기한다.


- 확률변수 x의 분산을 Var(X) 혹은 V(X)로 표기하는데, 기댓값의 표시방법에 의하여 위와같이 표시할 수 있다.

- 위 식이 유도되는 과정에서 ∑x f(x)는 모평균으로 이기 때문에 -2μ∑xf(x)는 -2 μ^2이 된다.
- ∑f(x) 는 전부 더하면 1이 되기 때문에 μ^2는 그대로 μ^2가 된다.
- 따라서 최종적으로 분산은 x제곱의 기댓값 - x의 기댓값의 제곱을 대입하여 계산할 수 있다.

- 표준편차는 분산에 루트를 취해서 스케일을 같게 만들어준 것이다.
- 마찬가지로 모집단의 표준편차는 모분산에 루트를 취한 것이며 위와같이 표기한다.
예제
- 동전 세 개를 던지기: 앞면의 수 X

- 이산균일분포

- 이산균일분포는 가질 수 있는 값에 해당되는 확률이 동일한 경우이다.
- 각각의 원소의 확률이 동일한 경우
연속확률변수 X의 분산

- 연속확률변수 X의 분산은 이산확률변수에서 ∑를 ∫로, f(x)를 f(x)dx [단위길이 dx 곱해줌]로 바꾸어 계산한다.


- 연속확률변수에서도 계산식에 대입하여 계산할 수 있다.
분산의 성질

- 위치의 변화룰 주는 상수 b는 분산에 영향을 주지 않음
- 분산은 퍼져있는 정도를 나타내는 값으로 어떤 위치에 있든지 영향을 받지 않음
- 분산은 측정단위의 제곱이기 때문에 a와 같이 척도에 변화를 주는 경우 a 제곱을 곱함

- 표준편차는 분산의 제곱근이지만 a가 음수일수도 있으니 주의해야됨

- U(0, 1)은 uniform distribution으로 균일분포, 균등분포이며, 해당 의미는 0과 1사이에서 균일한 분포를 갖는다는 것
- 따라서 E(X)는 0과 1사이의 균등한 분포이기 때문에 1/2이다.
- 12X를 Y라고 할 때, 12의 제곱으로하여 간단하게 구할 수 있다.
- W를 U(-1,1)이라고 할 때, x가 0~1 인 것에 2를 곱하면 0~2가 되고, 여기에 각각 -1을 하면 -1~1이 되기 때문에 W = 2X-1로 표현할 수 있다.
- 그렇게 하면 2X의 분산인 4Var(X)로 계산할 수 있다.
- 선형으로 표시되는 것들은 원리를 이용하여 쉽게 계산 가능하다.
요약
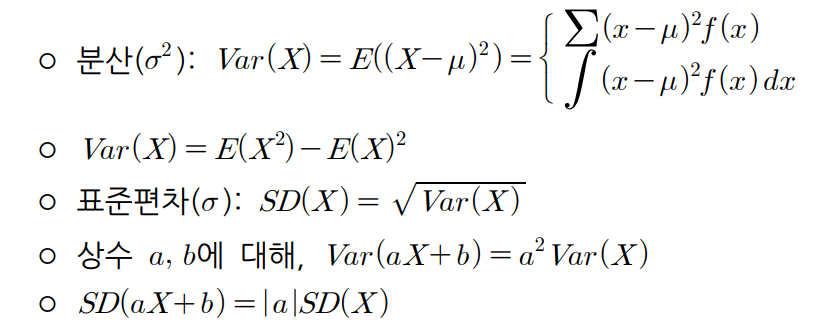
- 모분산을 계산하는 방법은 표본분산을 계산하는 것에서 n을 크게 하는 것으로 유추할 수 있다.
- 이산형과 연속형은 각각 ∑와 ∫로 계산할 수 있다.
- 표준편차는 분산에 루트를 취하여 구할 수 있다.
- 선형형태의 분산에서 위치에만 영향을 추는 상수 b는 분산에 영향을 주지 않는다.
- 척도에 변화를 줄 수 있는 a는 제곱을 한다.
- 표준편차를 계산할 때 주의할 점은 a에 절댓값을 취하는 것이다.
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 8주차 확률벡터 -3. 공분산과 상관계수 (0) | 2024.02.11 |
|---|---|
| [통계학의 이해Ⅰ] 8주차 확률벡터 -2. 결합분포와 주변분포 (0) | 2024.02.05 |
| [통계학의 이해Ⅰ] 7주차 확률변수와 확률분포 -5. 확률분포 퀴즈 (0) | 2024.02.04 |
| [통계학의 이해Ⅰ] 7주차 확률변수와 확률분포 -4. 확률변수의 기댓값 (0) | 2024.02.02 |
| [통계학의 이해Ⅰ] 7주차 확률변수와 확률분포 -3. 연속확률변수와 확률밀도함수 (0) | 2024.02.02 |



