[통계학의 이해Ⅰ] 7주차 확률변수와 확률분포 -2. 이산확률변수와 확률질량함수

해당 글은 숙명여자대학교 여인권 교수님의

K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.

추가적으로 여인권 교수님의 통계학 기본개념과 원리 2판을 참고하였습니다.

K-MOOC 사이트 링크 공유합니다.

---

학습목표

• 이산확률변수의 확률 구조를 나타내는 확률질량함수와 그 성질에 대해 알아본다.

---

확률질량함수(probability mass function)

• 이산확률변수: 확률변수의 치역이 셀 수 있는 경우
• 이산확률변수 X가 임의의 값 x일 확률 = P(X=x)

통계학의 이해Ⅰ 강의 자료 7-2의 페이지1

• 이산확률변수에 대한 확률 구조를 나타내는 것
• X가 이산확률변수이면 X가 x값일 확률이며 이때 f(x)를 확률질량함수라고 함

예제

통계학의 이해Ⅰ 강의 자료 7-2의 페이지2

통계학의 이해Ⅰ 강의 자료 7-2의 페이지3

• 젖혀진 윷이 나올 때까지 던지는 사건에서 x는 1, 2, 3... 무한대까지 가능함
• 이러한 현상을 확률질량함수로 표현할 수 있으며 이러한 형태를 "기하분포"라고 함
• 기하분포는 x가 커짐에 따라 확률이 기하급수적으로 작아지는 분포

확률질량함수의 성질

통계학의 이해Ⅰ 강의 자료 7-2의 페이지4

• 확률질량함수 f(x)는 확률변수 X가 임의의 상수 x일 확률이며, 확률이기 때문에 확률의 공리에 따라 항상 0과 1사이다.
• x가 임의의 a와 b사이에 있을 경우 그 사이에 있는 값들을 다 더하면 해당되는 확률을 구할 수 있다.
• 확률변수 X가 임의의 x보다 작거나 같을 확률을 고려할 수 있는데, 이러한 경우는 누적분포함수(cumulative distribution function)이라고 한다.

통계학의 이해Ⅰ 강의 자료 7-2의 페이지5

• 확률변수 X가 어떤 상수 x보다 작거나 같은 확률을 다 더한 것
• 표현할 때 대문자 F를 사용하여 F(x)라고 표현한다.

통계학의 이해Ⅰ 강의 자료 7-2의 페이지6 (누적분포함수)

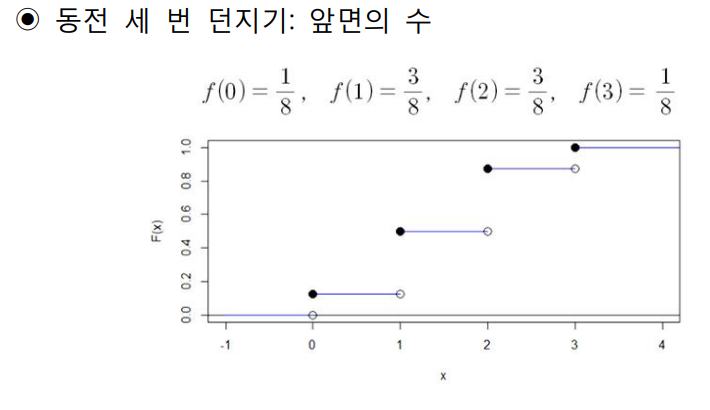
• 누적분포함수에서는 점프하는 구간이 그 지점에서의 확률

확률변수의 변환(transformation)

• 수학적으로 함수의 함수도 함수인 것처럼 확률변수의 함수 또한 새로운 확률변수가 될 수 있음
• 확률변수의 변환(함수) → 확률변수의 함수도 확률변수
• 변환된 확률변수의 확률분포 유도 가능

통계학의 이해Ⅰ 강의 자료 7-2의 페이지8

• X의 확률변수가 존재한다고 할 때, 확률변수 X에 관심이 있는 것이 아닌 X의 제곱에 관심있는 경우
• 1의 경우 기존 확률변수에는 2개가 가능하기 때문에 2개의 확률을 더해주는 방식
• 새로운 변수의 값에 해당되는 값이 기존의 확률변수의 값에 연결시키는 것
• 이를 확률변수의 변환, 변환된 확률변수의 확률분포라고 함

---

요약

통계학의 이해Ⅰ 강의 자료 7-2의 페이지10

• 변환된 확률변수의 질량함수인 경우에는 W에 해당되는 x들이 모두 존재
• 하나일수도 여러 개일 수 도 있음
• 여러 개인 경우 다 더하여 변환된 확률변수의 질량함수로 계산 가능