공부하는 블로그
[통계학의 이해Ⅰ] 2주차 일변량 자료 기술통계 -4. 기술통계 실습 (R)-과제 본문
728x90
해당 글은 숙명여자대학교 여인권 교수님의
K-MOOC 통계학의 이해Ⅰ(2019.05.01~2019.08.03) 강의를 수강하며 복습 및 정리하기 위해 작성한 글입니다.
과제
과제1
- "Score.txt"의 자료를 불러오기 (학점자료)
- 도수분포표 만들기: 도수, 상대도수, 누적상대도수 포함
# score file scan
score <- scan("score.txt", what="character")
## 도수분포표 구하기
scoreTable <- table(score)
scoreTable <- scoreTable[c("A+","A","B+","B","C+","C","D+","D","F")]
Total <- sum(scoreTable)
ScoreProp <- 100*scoreTable/Total
ScoreProp <- round(ScoreProp,1)
ScoreProp <- ScoreProp[c("A+","A","B+","B","C+","C","D+","D","F")]
CumScoreProp <- cumsum(ScoreProp)
ScoreFreq <- cbind(scoreTable,ScoreProp, CumScoreProp)
colnames(ScoreFreq) <- c("도수","상대도수", "누적상대도수")
print(ScoreFreq)
- 막대그래프 그리기: 상대도수 표시
## 막대그래프 그리기
barplot(ScoreFreq[,2], ylim=c(0,30),space=0.5,
main = "학점 막대그래프", xlab = "학점", ylab = "상대도수(%)")
abline(h=0)
abline(h=c(10,20,30),lty=3)
과제2
- 취업률 자료에 대하여 (,]와 [,) 비교
- 도수분포표와 히스토그램 비교
## 취업률
Job <- scan()
# 아래 데이터 직접 입력력
# 55.6 83.3 43.4 58.1 31.6 55.6 60.7 64.6 73.3 55.6 64.3
# 52.8 22.7 46.3 71.4 53.8 64.5 67.9 71.4 80.0 59.5 40.5
# 77.1 58.6 65.4 52.4 66.7 91.3 41.3 72.1 61.9 78.4 63.6
# 41.0 65.2 81.3 54.8 19.6 50.0 53.1 41.2 56.5
# 도수 분포표 구하기: [, ) 이상, 미만
JobCut <- cut(Job, breaks=c(10, 39.9, 49.9, 59.9, 69.9, 79.9, 100), rgiht = TRUE)
JobFreq <- table(JobCut)
JobProp <- round(JobFreq/sum(JobFreq),3)
CumJobProp <- cumsum(JobProp)
Result <- cbind(JobFreq,JobProp,CumJobProp)
colnames(Result) <- c("도수","상대도수","누적상대도수")
rownames(Result) <- c("10%~40%","40%~50%","50%~60%",
"60%~70%","70%~80%","80%~100%")
print(Result)
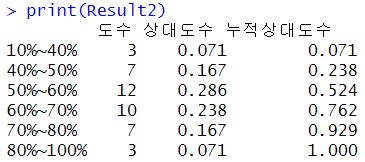
# 도수 분포표 구하기: (, ] 초과, 이하
JobCut2 <- cut(Job, breaks=c(10, 40.1, 50.1, 60.1, 70.1, 80.1, 100.1))
JobFreq2 <- table(JobCut2)
JobProp2 <- round(JobFreq2/sum(JobFreq2),3)
CumJobProp2 <- cumsum(JobProp2)
Result2 <- cbind(JobFreq2,JobProp2,CumJobProp2)
colnames(Result2) <- c("도수","상대도수","누적상대도수")
rownames(Result2) <- c("10%~40%","40%~50%","50%~60%",
"60%~70%","70%~80%","80%~100%")
print(Result2)
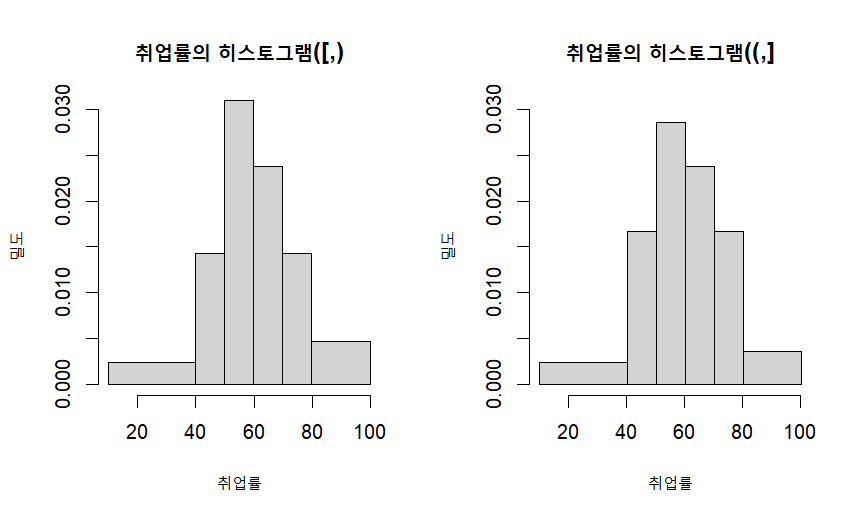
# 취업률 히스토그램 비교교
par(mfrow=c(1,2))
hist(Job,freq=FALSE, main = "취업률의 히스토그램((,])", xlab = "취업률", ylab = "밀도",
breaks=c(10, 39.9, 49.9, 59.9, 69.9, 79.9, 100), ylim = c(0,0.03))
hist(Job,freq=FALSE, main = "취업률의 히스토그램([,)", xlab = "취업률", ylab = "밀도",
breaks=c(10, 40.1, 50.1, 60.1, 70.1, 80.1, 100.1), ylim =c(0,0.03))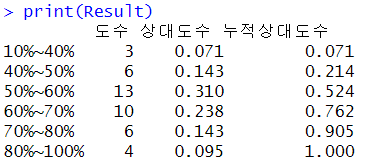
※ 강좌는 청강한 것이라 과제 검토받지 못하였습니다. 학습한 내용 기반으로 작성한 것이므로 정답인지 아닌지 알 수 없습니다.
'통계 > 통계학의 이해Ⅰ' 카테고리의 다른 글
| [통계학의 이해Ⅰ] 3주차 일변량 자료에 대한 수치적 기술통계 -2. 수치자료의 대체중심위치 (4) | 2024.01.13 |
|---|---|
| [통계학의 이해Ⅰ] 3주차 일변량 자료에 대한 수치적 기술통계 -1. 수치자료 분포의 중심위치 - 평균 (0) | 2024.01.13 |
| [통계학의 이해Ⅰ] 2주차 일변량 자료 기술통계 -3. 수치 자료 정리 (4) | 2024.01.06 |
| [통계학의 이해Ⅰ] 2주차 일변량 자료 기술통계 -2. 범주형 자료 정리 (0) | 2024.01.06 |
| [통계학의 이해Ⅰ] 2주차 일변량 자료 기술통계 -1. 자료의 분류와 특성 (0) | 2024.01.01 |




